题目内容
已知函数f(x)=e
(e是自然对数的底数).
(1)若函数f(x)是(-1,+∞)上的增函数,求k的取值范围;
(2)若对任意的x∈(0,+∞),都有f(x)<x+1,求满足条件的最大整数k的值.
| kx-1 |
| x+1 |
(1)若函数f(x)是(-1,+∞)上的增函数,求k的取值范围;
(2)若对任意的x∈(0,+∞),都有f(x)<x+1,求满足条件的最大整数k的值.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,导数的综合应用
分析:(1)设g(x)=
,求出导数,再由单调性可得g(x))是(-1,+∞)上的增函数,运用导数大于0,即可得到;
(2)先猜想满足条件的最大整数k=2.再证明,设h(x)=ln(x+1)+
,再由导数判断单调性,再由单调性得到h(x)≥h(2),即可得证.
| kx-1 |
| x+1 |
(2)先猜想满足条件的最大整数k=2.再证明,设h(x)=ln(x+1)+
| 3 |
| x+1 |
解答:
解:(1)设g(x)=
,导数g′(x)=
=
由于f(x))是(-1,+∞)上的增函数,且e>1,则g(x))是(-1,+∞)上的增函数,
即有g′(x)>0,即有k>-1,即k的取值范围是(-1,+∞);
(2)由条件可得,f(1)<2,即e
<2,即有k<1+2ln2<3,猜想满足条件的最大整数k=2.
证明:对任意的x∈(0,+∞),都有f(x)<x+1.
e
<x+1?2-
<ln(x+1)?ln(x+1)+
>2,
设h(x)=ln(x+1)+
,则h′(x)=
-
=
当0<x<2时,h′(x)<0,当x>2时,h′(x)>0,
则?x>0,则h(x)≥h(2)=1+ln3>2,
即有对任意的x∈(0,+∞),都有f(x)<x+1.
则满足条件的最大整数k=2.
| kx-1 |
| x+1 |
| k(x+1)-kx+1 |
| (x+1)2 |
| k+1 |
| (x+1)2 |
由于f(x))是(-1,+∞)上的增函数,且e>1,则g(x))是(-1,+∞)上的增函数,
即有g′(x)>0,即有k>-1,即k的取值范围是(-1,+∞);
(2)由条件可得,f(1)<2,即e
| k-1 |
| 2 |
证明:对任意的x∈(0,+∞),都有f(x)<x+1.
e
| 2x-1 |
| x+1 |
| 3 |
| x+1 |
| 3 |
| x+1 |
设h(x)=ln(x+1)+
| 3 |
| x+1 |
| 1 |
| x+1 |
| 3 |
| (x+1)2 |
| x-2 |
| (x+1)2 |
当0<x<2时,h′(x)<0,当x>2时,h′(x)>0,
则?x>0,则h(x)≥h(2)=1+ln3>2,
即有对任意的x∈(0,+∞),都有f(x)<x+1.
则满足条件的最大整数k=2.
点评:本题考查导数的运用:求单调区间和判断单调性,考查不等式恒成立思想,以及单调性的运用,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
已知函数f(x)=
,则f[f(3)]=( )
|
| A、-3 | B、3 | C、-9 | D、9 |
若
,
,
均为单位向量,且
•
=0,(
+
)•
≥
2,则|
+
+
|的最小值为( )
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
| c |
| a |
| b |
| c |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
已知圆台的上下底面半径分别为1和2,高为1,则该圆台的全面积为( )
A、3
| ||||
B、(5+3
| ||||
C、
| ||||
D、
|
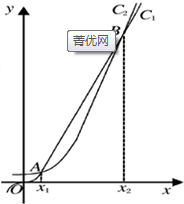 函数f(x)=2x和g(x)=x3的图象的示意图如下图所示.设两个函数的图象交于点A(x1,y1),B,2,y2)且x1<x2.
函数f(x)=2x和g(x)=x3的图象的示意图如下图所示.设两个函数的图象交于点A(x1,y1),B,2,y2)且x1<x2.