题目内容
一个盒子中有5个大小、形状完全相同的小球,其中2个球的标号是不同的偶数,其余球的标号是不同的奇数,现从中任取3个球,则这3个球的标号之和是偶数的概率为 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:由题意知本题是一个等可能事件的概率,记5个球分别为:1,2,3,4,5;用列举法可得基本事件数,进而可得答案.
解答:
解:由题意知本题是一个等可能事件的概率,记5个球分别为:1,2,3,4,5,(2个偶数3个奇数);
试验发生包含的事件是从5个球中取3个球,共有:
(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),
(1,4,5),(2,3,4),(2,3,5),(2,4,5),(3,4,5),10种结果,
满足条件的事件是3个球的标号之和是偶数,包括:
(1,2,3),(1,2,5),(1,3,4),(1,4,5),(2,3,5),(3,4,5),共6种结果,
根据等可能事件的概率公式得到P=
=
,
故答案为:
.
试验发生包含的事件是从5个球中取3个球,共有:
(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),
(1,4,5),(2,3,4),(2,3,5),(2,4,5),(3,4,5),10种结果,
满足条件的事件是3个球的标号之和是偶数,包括:
(1,2,3),(1,2,5),(1,3,4),(1,4,5),(2,3,5),(3,4,5),共6种结果,
根据等可能事件的概率公式得到P=
| 6 |
| 10 |
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:本题考查等可能事件的概率,准确列举基本事件数是解决问题的关键,属基础题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
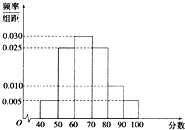 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40、50),[50、60),[60、70),[70、80),[80、90),[90、100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40、50),[50、60),[60、70),[70、80),[80、90),[90、100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )