题目内容
12.已知抛物线y2=4x的准线与双曲线4x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)交于A、B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线离心率为( )| A. | $\frac{\sqrt{17}}{2}$ | B. | $\frac{\sqrt{15}}{3}$ | C. | $\frac{\sqrt{57}}{3}$ | D. | $\frac{8}{3}$ |
分析 根据抛物线的方程求出抛物线的准线方程和焦点坐标,结合直角三角形的性质建立方程关系进行求解即可.
解答 解:由抛物线的标准方程得抛物线的准线为x=-1,抛物线的焦点F(1,0),
将x=-1代入双曲线方程得4-$\frac{{y}^{2}}{{b}^{2}}$=1,即$\frac{{y}^{2}}{{b}^{2}}$=3,则y=±$\sqrt{3}$b,
设A(-1,$\sqrt{3}$b),B(-1,-$\sqrt{3}$b),
∵△FAB为直角三角形,
∴tan45°=$\frac{\sqrt{3}b}{2}$=1,则b=$\frac{2}{\sqrt{3}}$,
则双曲线的方程为4x2-$\frac{{y}^{2}}{\frac{4}{3}}$=1,
即$\frac{{x}^{2}}{\frac{1}{4}}$-$\frac{{y}^{2}}{\frac{4}{3}}$=1,则a=$\frac{1}{2}$,
c=$\sqrt{\frac{1}{4}+\frac{4}{3}}$=$\frac{\sqrt{57}}{6}$,
则双曲线的离心率e=$\frac{c}{a}$=$\frac{\frac{\sqrt{57}}{6}}{\frac{1}{2}}$=$\frac{\sqrt{57}}{3}$,
故选:C.
点评 本题主要考查双曲线离心率的计算,根据抛物线和双曲线的性质建立方程是解决本题的关键.

练习册系列答案
相关题目
2.已知A∈α,AB=5,$AC=2\sqrt{2}$,且AB与α所成角的正弦值为$\frac{4}{5}$,AC与α所成的角为45°,点B,C在平面α同侧,则BC长的范围为( )
| A. | $[5-2\sqrt{2},5+2\sqrt{2}]$ | B. | $[\sqrt{5},\sqrt{29}]$ | C. | $[\sqrt{5},\sqrt{61}]$ | D. | $[\sqrt{29},\sqrt{61}]$ |
3.已知函数f(x)=x2-2ax+5(a>1),g(x)=log3x,若函数f(x)的定义域与值域都是[1,a],则对于任意的x1,x2∈[1,a+1]时,总有$|{f({x_1})-g({x_2})}|≤{t^2}+2t-1$恒成立,则t的取值范围为( )
| A. | [1,3] | B. | [-1,3] | C. | [1,+∞)∪(-∞,-3] | D. | [3,+∞)∪(-∞,-1] |
20.已知圆C:x2+y2+2x-3=0,直线l:x+ay+2-a=0(a∈R),则( )
| A. | l与C相离 | B. | l与C相切 | ||
| C. | l与C相交 | D. | 以上三个选项均有可能 |
1.执行如图所示的程序框图,则输出s的值为( )
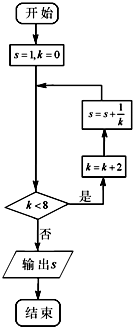

| A. | $\frac{3}{2}$ | B. | $\frac{7}{4}$ | C. | $\frac{23}{12}$ | D. | $\frac{49}{24}$ |
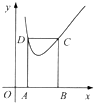 如图,矩形ABCD的边AB在x轴上,顶点C,D在函数y=x+$\frac{1}{x}({x>0})$的图象上.记AB=m,BC=n,则$\frac{m}{n^2}$的最大值为$\frac{1}{4}$.
如图,矩形ABCD的边AB在x轴上,顶点C,D在函数y=x+$\frac{1}{x}({x>0})$的图象上.记AB=m,BC=n,则$\frac{m}{n^2}$的最大值为$\frac{1}{4}$.