题目内容
1.对于函数f(x),定义域为D,若存在x0∈D使f(x0)=x0,则称(x0,x0)为f(x)的图象上的不动点,由此,函数f(x)=4x+2x-2的零点差绝对值不超过0.25,则满足条件的g(x)有①②.①g(x)=4x-1;②$g(x)={({x-\frac{1}{2}})^2}$;③g(x)=ex-1;④$g(x)=ln({\frac{π}{x}-3})$.
分析 先判断g(x)的零点所在的区间,再求出各个选项中函数的零点,看哪一个能满足与g(x)=4x+2x-2的零点之差的绝对值不超过0.25.
解答 解:∵f(x)=4x+2x-2在R上连续,且f($\frac{1}{4}$)=$\sqrt{2}$+$\frac{1}{2}$-2=$\sqrt{2}$-$\frac{3}{2}$<0,f($\frac{1}{2}$)=2+1-2=1>0.
设f(x)=4x+2x-2的零点为x0,则$\frac{1}{4}$<x0<$\frac{1}{2}$,
0<x0-$\frac{1}{4}$<$\frac{1}{4}$,∴|x0-$\frac{1}{4}$|<$\frac{1}{4}$.
又g(-x)=4x-1零点为x=$\frac{1}{4}$;
$g(x)={({x-\frac{1}{2}})^2}$的零点为x=$\frac{1}{2}$;
g(x)=ex-1零点为x=0;
$g(x)=ln({\frac{π}{x}-3})$零点为x=$\frac{π}{4}$,
满足题意的函数有①②.
故答案为:①②.
点评 本题考查判断函数零点所在的区间以及求函数零点的方法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.直线2x-y+4=0同时过第( )象限.
| A. | 一,二,三 | B. | 二,三,四 | C. | 一,二,四 | D. | 一,三,四 |
16.已知a=log30.2,b=30.2,c=0.30.2,则a,b,c三者的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
6.根据如下样本数据得到的回归方程为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,若$\stackrel{∧}{a}$=4.5,则x每增加1个单位,y就( )
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4 | 2.5 | -0.5 | 0.5 | -2 |
| A. | 增加0.9个单位 | B. | 减少0.9个单位 | C. | 增加0.72个单位 | D. | 减少0.72个单位 |
19.如图所示,在?ABCD中,AE:EB=1:2,若S△AEF=6cm2,则S△CDF为( )
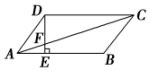

| A. | 54 cm2 | B. | 24 cm2 | C. | 18 cm2 | D. | 12 cm2 |
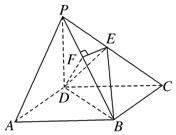 如图,在四棱锥P-ABCD中,ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.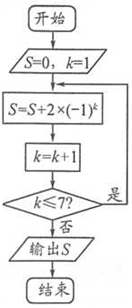 已知某算法的程序框图如图所示,则输出的S的值是-2.
已知某算法的程序框图如图所示,则输出的S的值是-2.