题目内容
已知回归直线的斜率的估计值是2,样本点的中心为(4,12),则回归直线的方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:线性回归方程
专题:综合题,概率与统计
分析:本题考查线性回归直线方程,可根据回归直线方程一定经过样本中心点这一信息,选择验证法或排除法解决,具体方法就是将点(4,12)的坐标分别代入各个选项,满足的即为所求.
解答:
解:由回归直线的斜率的估计值为2,可排除B、D
由线性回归直线方程样本点的中心为(4,12),
将x=4分别代入A、C,其值依次为12,-12,排除C.
故选:A.
由线性回归直线方程样本点的中心为(4,12),
将x=4分别代入A、C,其值依次为12,-12,排除C.
故选:A.
点评:本题运用了样本中心点的坐标满足回归直线方程.

练习册系列答案
相关题目
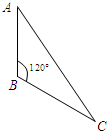 在△ABC中,AB=3,BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,则所形成的几何体的体积是( )
在△ABC中,AB=3,BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,则所形成的几何体的体积是( )| A、11π | B、12π |
| C、13π | D、14π |
现要制作一个圆锥形的漏斗,其母线长为l,要使其体积最大,高应为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、1 | ||
B、
| ||
C、
| ||
D、
|
cos600°=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
复数(1-i)2的虚部是( )
| A、-2i | B、2 | C、-2 | D、0 |
