题目内容
对于以下说法:
(1)命题“已知x,y∈R”,若x≠2或y≠3,则“x+y≠5”是真命题;
(2)设f(x)的导函数为f′(x),若f′(x0)=0,则x0是函数f(x)的极值点;
(3)对于函数f(x),g(x),f(x)≥g(x)恒成立的一个充分不必要的条件是f(x)min≥g(x)max;
(4)若定义域为R的函数y=f(x),满足f(x)+f(4-x)=2,则其图象关于点(2,1)对称.
其中正确的说法序号是 .
(1)命题“已知x,y∈R”,若x≠2或y≠3,则“x+y≠5”是真命题;
(2)设f(x)的导函数为f′(x),若f′(x0)=0,则x0是函数f(x)的极值点;
(3)对于函数f(x),g(x),f(x)≥g(x)恒成立的一个充分不必要的条件是f(x)min≥g(x)max;
(4)若定义域为R的函数y=f(x),满足f(x)+f(4-x)=2,则其图象关于点(2,1)对称.
其中正确的说法序号是
考点:命题的真假判断与应用
专题:阅读型,函数的性质及应用,导数的综合应用,简易逻辑
分析:原命题与其逆否命题是等价命题,写出命题的逆否命题,即可判断(1);
极值点的导数为0,但导数为0的点不一定为极值点.比如y=x3,在x=0的点不是极值点,即可判断(2);
对于函数f(x),g(x)若满足f(x)min≥g(x)max恒成立,则f(x)≥g(x)恒成立,若f(x)≥g(x)恒成立,不一定有f(x)min≥g(x)max,比如f(x)=x+2,g(x)=x+1,即可判断(3);
若f(x)+f(2a-x)=2b,则函数y=f(x)的图象关于点(a,b)对称,即可判断(4).
极值点的导数为0,但导数为0的点不一定为极值点.比如y=x3,在x=0的点不是极值点,即可判断(2);
对于函数f(x),g(x)若满足f(x)min≥g(x)max恒成立,则f(x)≥g(x)恒成立,若f(x)≥g(x)恒成立,不一定有f(x)min≥g(x)max,比如f(x)=x+2,g(x)=x+1,即可判断(3);
若f(x)+f(2a-x)=2b,则函数y=f(x)的图象关于点(a,b)对称,即可判断(4).
解答:
解:对于(1),原命题与其逆否命题是等价命题,
若x≠2或y≠3,则x+y≠5的逆否命题是:若x+y=5,则x=2且y=3是假命题,故(1)错误;
对于(2),极值点的导数为0,但导数为0的点不一定为极值点.
比如y=x3,在x=0的点不是极值点,故(2)错;
对于(3),对于函数f(x),g(x)若满足f(x)min≥g(x)max恒成立,则f(x)≥g(x)恒成立,
若f(x)≥g(x)恒成立,不一定有f(x)min≥g(x)max,比如f(x)=x+2,g(x)=x+1,故(3)正确;
对于(4),若f(x)+f(2a-x)=2b,则函数y=f(x)的图象关于点(a,b)对称,故(4)正确.
故答案为:(3)(4).
若x≠2或y≠3,则x+y≠5的逆否命题是:若x+y=5,则x=2且y=3是假命题,故(1)错误;
对于(2),极值点的导数为0,但导数为0的点不一定为极值点.
比如y=x3,在x=0的点不是极值点,故(2)错;
对于(3),对于函数f(x),g(x)若满足f(x)min≥g(x)max恒成立,则f(x)≥g(x)恒成立,
若f(x)≥g(x)恒成立,不一定有f(x)min≥g(x)max,比如f(x)=x+2,g(x)=x+1,故(3)正确;
对于(4),若f(x)+f(2a-x)=2b,则函数y=f(x)的图象关于点(a,b)对称,故(4)正确.
故答案为:(3)(4).
点评:本题考查四种命题的真假及充分必要条件的判断,函数的导数与极值的关系,函数的最值和对称性,属于易错题,和中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
若(2-3x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则|a0|+|a1|+|a2|+|a3|+|a4|+|a5|等于( )
| A、55 |
| B、-1 |
| C、25 |
| D、-25 |
已知函数y=f(x)是定义在R上的偶函数,且当x>0时,不等式f(x)+x•f′(x)<0成立,若a=30.2•f(30.2),b=(logπ2)•f(logπ2),c=(log2
)•f (log2
),则a,b,c间的大小关系( )
| 1 |
| 4 |
| 1 |
| 4 |
| A、c>b>a |
| B、c>a>b |
| C、b>a>c |
| D、a>c>b |
在△ABC中,已知三边a=3,b=5,c=7,则三角形ABC是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |
89×90×91×92×…×100可表示为( )
A、A
| ||
B、
| ||
C、
| ||
D、
|
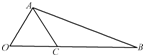 如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,试求:
如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,试求: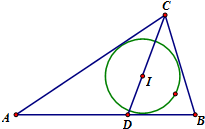 如图,△ABC中,点A(-1,0),B(1,0).圆I是△ABC的内切圆,且CI延长线交AB与点D,若
如图,△ABC中,点A(-1,0),B(1,0).圆I是△ABC的内切圆,且CI延长线交AB与点D,若