题目内容
已知y=f-1(x)是函数f(x)=arcsin(1-x)的反函数,则f-1(x)= .
考点:反函数
专题:函数的性质及应用
分析:按照求反函数的基本步骤,(1)用含y的解析式表示x,(2)交换x、y的位置,(3)求出反函数的定义域(即原函数的值域),求出函数f(x)的反函数f-1(x).
解答:
解:∵f(x)=arcsin(1-x),
∴siny=1-x,y∈[-
,
],
∴x=1-siny,y∈[-
,
];
交换x、y的位置,
得y=1-sinx,x∈[-
,
];
∴f(x)的反函数是f-1(x)=1-sinx,x∈[-
,
].
故答案为:1-sinx,x∈[-
,
].
∴siny=1-x,y∈[-
| π |
| 2 |
| π |
| 2 |
∴x=1-siny,y∈[-
| π |
| 2 |
| π |
| 2 |
交换x、y的位置,
得y=1-sinx,x∈[-
| π |
| 2 |
| π |
| 2 |
∴f(x)的反函数是f-1(x)=1-sinx,x∈[-
| π |
| 2 |
| π |
| 2 |
故答案为:1-sinx,x∈[-
| π |
| 2 |
| π |
| 2 |
点评:本题考查了求反函数的问题,解题时应按照求反函数的基本步骤,求出函数f(x)的反函数f-1(x)即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若△ABC的内角A,B,C满足
=
=
,则cosB=( )
| 2 |
| sinA |
| 3 |
| sinB |
| 4 |
| sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知等差数列{an}的前n项和为Sn,若S10=
(6x+
)dx,则a3+a8=( )
| ∫ | 2 0 |
| 3 |
| 2 |
| A、3 | B、6 | C、9 | D、12 |

 如图,AB是圆O的直径,AB=2,D为圆O上一点,过D作圆O的切线交AB的延长线于点C.若DA=DC,则∠BDC=
如图,AB是圆O的直径,AB=2,D为圆O上一点,过D作圆O的切线交AB的延长线于点C.若DA=DC,则∠BDC=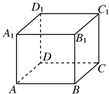 如图所示,在正方体ABCD-A1B1C1D1中,下列各式中运算结果为向量
如图所示,在正方体ABCD-A1B1C1D1中,下列各式中运算结果为向量