题目内容
已知复数z1=1+3i，z2=3+i（i为虚数单位）．在复平面内，z1-z2对应的点在第 象限．
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：利用复数的运算法则、几何意义即可得出．
解答：
解：∵复数z1=1+3i，z2=3+i，
∴z1-z2=（1+3i）-（3+i）=-2+2i，对应的点为（-2，2）．
∴在复平面内，z1-z2对应的点在第 二象限．
故答案为：二．
∴z1-z2=（1+3i）-（3+i）=-2+2i，对应的点为（-2，2）．
∴在复平面内，z1-z2对应的点在第 二象限．
故答案为：二．
点评：本题考查了复数的运算法则、几何意义，属于基础题．
练习册系列答案
相关题目
已知an=2，amn=16，则m的值为（ ）
| A、3 |
| B、4 |
| C、a3 |
| D、a6 |
设集合A={x|y=lg（x-3）}，B={x|x2-5x+5＜0}，则A∩B=（ ）
| A、∅ | ||||
B、（3，
| ||||
| C、（-2，1） | ||||
| D、（4，+∞） |
函数f（x）=ln（1+x）+
的定义域为（ ）
| ||
| x |
| A、（-1，0）∪（0，1] |
| B、（-1，1） |
| C、（-1，1] |
| D、[-1，0）∪（0，1] |
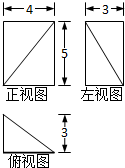
已知椭圆C1：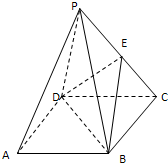
，底面BCD是直角梯形，AB∥CD，∠ADC=90°，AB=AD=PD=1，CD=2．