题目内容
已知椭圆的对称轴为坐标轴,左、右两个焦点分别为F1、F2,且抛物线y2=4
x与该椭圆有一个共同的焦点,点P在椭圆C上,且PF2⊥F1F2,|PF1|=
.
(1)求椭圆C的方程;
(2)设D(
,0),过F2且不垂直于坐标轴的动直线l交椭圆C于A、B两点,若以DA、DB为邻边的平行四边形为菱形,求直线l的方程.
| 3 |
| 7 |
| 2 |
(1)求椭圆C的方程;
(2)设D(
| ||
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出c=
,|F1F2|=2
,从而得到|PF2|=
,由此能求出椭圆C的方程.
(2)设A(x1,y1),B(x2,y2),直线AB为:y=k(x-
),联立
,得(1+4k2)x2-8
k2x+12k2-4=0,由此利用韦达定理结合已知条件能求出直线l的方程.
| 3 |
| 3 |
| 1 |
| 2 |
(2)设A(x1,y1),B(x2,y2),直线AB为:y=k(x-
| 3 |
|
| 3 |
解答:
解:(1)∵抛物线y2=4
x的焦点坐标F(
,0),∴c=
,
∴|F1F2|=2
,
∵|PF1|=
,PF2⊥F1F2,
∴|PF2|=
=
,
∴2a=|PF1|+|PF2|=4,∴b=
=1,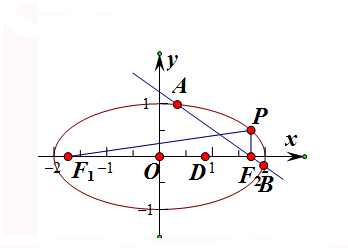
∴椭圆C的方程为:
+y2=1.
(2)设A(x1,y1),B(x2,y2),直线AB为:y=k(x-
),
联立
,
消去y,并整理,得(1+4k2)x2-8
k2x+12k2-4=0,
x1+x2=
,
y1+y2=k(
+x2)-2
k=-
,
∵AD=BD,
∴(x1-
)2+y12=(x2-
)2+y22,
=-
=
=k,
解得k=±
,
∴直线AB为y=±
(x-
).
| 3 |
| 3 |
| 3 |
∴|F1F2|=2
| 3 |
∵|PF1|=
| 7 |
| 2 |
∴|PF2|=
(
|
| 1 |
| 2 |
∴2a=|PF1|+|PF2|=4,∴b=
22-(
|

∴椭圆C的方程为:
| x2 |
| 4 |
(2)设A(x1,y1),B(x2,y2),直线AB为:y=k(x-
| 3 |
联立
|
消去y,并整理,得(1+4k2)x2-8
| 3 |
x1+x2=
8
| ||
| 1+4k2 |
y1+y2=k(
| x | 1 |
| 3 |
2
| ||
| 1+4k2 |
∵AD=BD,
∴(x1-
| ||
| 2 |
| ||
| 2 |
| y2-y1 |
| x2-x1 |
x1+x2-
| ||
| y1+y2 |
| 4k2-1 |
| 2k |
解得k=±
| ||
| 2 |
∴直线AB为y=±
| ||
| 2 |
| 3 |
点评:本题考查椭圆方程的求法,考查直线方程的求法,考查推理论证能力,考查综合应用能力,解题时要熟练掌握椭圆性质.

练习册系列答案
相关题目
在下列四个选项中,说法错误的是( )
| A、若A是B的必要不充分条件,则非B也是非A的必要不充分条件 | |||||
B、“
| |||||
| C、“x≠1”是“x2≠1”的充分不必要条件 | |||||
| D、“x≠0”是“x+|x|>0”的必要不充分条件 |
 如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-
如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-