题目内容
已知椭圆
+
=1的右焦点为F1(3,0),设直线y=kx与椭圆相交于A、B两点,M、N分别为线段AF1,BF1的中点,若坐标原点O在以MN为直径的圆上,请运用椭圆的几何性质证明线段|AB|的长是定值.
| x2 |
| a2 |
| y2 |
| b2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:由椭圆的对称性知|OA|=|OB|,由已知条件推导出OM⊥ON,四边形ONF1M是平行四边形,由此能证明线段|AB|的长是定值.
解答:
证明:∵椭圆
+
=1=1的右焦点为F1(3,0),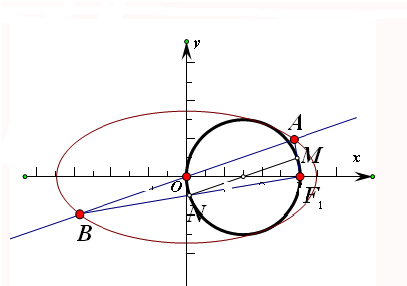
直线y=kx与椭圆相交于A、B两点,
∴由椭圆的对称性知|OA|=|OB|,
∵M、N分别为线段AF1,BF1的中点,
坐标原点O在以MN为直径的圆上,
∴OM⊥ON,OM∥NF1,ON∥MF1,
∴四边形ONF1M是平行四边形,
∴∠NF1M=90°,即∠AF1B=90°,
∴|AB|=2|OF1|=2×3=6,
∴线段|AB|的长是定值6.
| x2 |
| a2 |
| y2 |
| b2 |

直线y=kx与椭圆相交于A、B两点,
∴由椭圆的对称性知|OA|=|OB|,
∵M、N分别为线段AF1,BF1的中点,
坐标原点O在以MN为直径的圆上,
∴OM⊥ON,OM∥NF1,ON∥MF1,
∴四边形ONF1M是平行四边形,
∴∠NF1M=90°,即∠AF1B=90°,
∴|AB|=2|OF1|=2×3=6,
∴线段|AB|的长是定值6.
点评:本题考查线段长为定值的证明,是中档题,解题时要注意数形结合思想的合理运用.

练习册系列答案
相关题目
“实数a=1”是“复数(1+ai)i(a∈R,i为虚数单位)的模为
”的( )
| 2 |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不是充分条件又不是必要条件 |