题目内容
10.△ABC的内角A,B,C的对边分别为a,b,c,已知2c-a=2bcosA.(1)求角B的大小;
(2)若a=2,b=$\sqrt{7}$,求c的长.
分析 (1)根据正弦定理和两角和的正弦公式即可求出,
(2)利用余弦定理即可求出
解答 解:(1)∵2c-a=2bcosA,
由正弦定理可得2sinC-sinA=2sinBcosA,
∵sinC=sin(A+B)=sinAcosB+cosAsinB,
∴2sinAcosB+2cosAsinB-sinA=2sinBcosA
∴2sinAcosB=sinA
∵sinA≠0,
∴cosB=$\frac{1}{2}$,
∴B=$\frac{π}{3}$,
(2)由余弦定理可得b2=a2+c2-2accosB
∴7=4+c2-2c,
即c2-2c-3=0,
解得c=3或c=-1(舍去),
∴c=3.
点评 本题考查了正弦定理余弦定理,两角和的正弦公式和三角形的内角和定理,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.给定命题p:“若a2017>-1,则a>-1”;命题q:“?x∈R,x2tanx2>0”,则下列命题中,真命题的是( )
| A. | p∨q | B. | (¬p)∨q | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
5.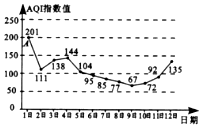 AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
 AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )| A. | 这12天中有6天空气质量为“优良” | B. | 这12天中空气质量最好的是4月9日 | ||
| C. | 这12天的AQI指数值的中位数是90 | D. | 从4日到9日,空气质量越来越好 |
15.复数$\frac{1}{1-i}$+$\frac{1}{1+i}$=( )
| A. | i | B. | -i | C. | -1 | D. | 1 |
2.设集合M={-2,2},N={x|x<0,或x>1},则下列结论正确的是( )
| A. | N⊆M | B. | M⊆N | C. | M∩N=N | D. | M∩N={2} |
20.在射击训练中,某战士射击了两次,设命题p是“第一次射击击中目标”,命题q是“第二次射击击中目标”,则命题“两次射击中至少有一次没有击中目标“为真命题的充要条件是( )
| A. | (¬p)∨(¬q)为真命题 | B. | p∨(¬q)为真命题 | C. | (¬p)∧(¬q)为真命题 | D. | p∨q为真命题 |
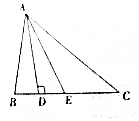 如图,在△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,求∠DAE与∠AEC的度数.
如图,在△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,求∠DAE与∠AEC的度数.