题目内容
1.给定命题p:“若a2017>-1,则a>-1”;命题q:“?x∈R,x2tanx2>0”,则下列命题中,真命题的是( )| A. | p∨q | B. | (¬p)∨q | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
分析 命题p:幂函数y=a2017,在R上单调递增,即可判断出真假.命题q:取x=$\sqrt{\frac{2π}{3}}$,则x2tanx2=$\frac{2π}{3}$tan$\frac{2π}{3}$<0,因此命题q是假命题.再利用复合真假的判定方法即可得出.
解答 解:命题p:幂函数y=a2017,在R上单调递增,因此若a2017>-1,则a>-1”,是真命题.
命题q:取x=$\sqrt{\frac{2π}{3}}$,则x2tanx2=$\frac{2π}{3}$tan$\frac{2π}{3}$=-$\frac{2\sqrt{3}π}{3}$<0,因此命题q是假命题.
则B,C,D都为假命题.
只有A是真命题.
故选:A.
点评 本题考查了函数的性质、不等式的解法、复合命题的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
9.将一条均匀木棍随机折成两段,则其中一段大于另一段三倍的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
10.如图所示,向量$\overrightarrow{O{Z_1}},\overrightarrow{O{Z_2}}$所对应的复数分别为Z1,Z2,则Z1•Z2=( )
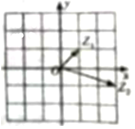

| A. | 4+2i | B. | 2+i | C. | 2+2i | D. | 3+i |
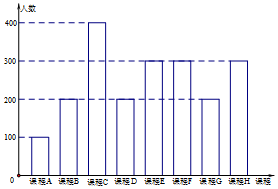 为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.图中,课程A,B,C,D,E为人文类课程,课程F,G,H为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组M”).
为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.图中,课程A,B,C,D,E为人文类课程,课程F,G,H为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组M”).