Question

求函数f（x）=

2-sinx

2+cosx

的值域．

Answer 1

考点：函数的最值及其几何意义,函数的值域

专题：函数的性质及应用

分析：可以把函数理解为点（-cosx，sinx）到点（2，2）的直线斜率的范围，利用数形结合的思想，求得过点（2，2）的直线与单位圆相切时直线的斜率，进而求得函数f（x）的值域．

解答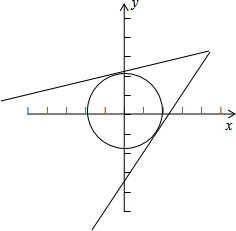： 解：可以把函数理解为点（-cosx，sinx）到点（2，2）的直线斜率的范围，
而（-cosx，sinx）的点的集合为以原点为圆心，半径为1的圆，如图：
当过点（2，2）的直线的斜率不存在时，不与圆相切，
设此直线的方程为y-2=k（x-2），整理得y-kx+2k-2=0，①
圆的方程为x²+y²=1，②
圆心到直线的距离为

|2k-2|

1+k2

=1，整理求得k=

4± 7

3

，
∴函数f（x）=

2-sinx

2+cosx

的值域：[

4- 7

3

，

4+ 7

3

]．

点评：本题主要考查了直线与圆的位置关系，三角函数化简求值的问题．考查了学生转化与化归思想的运用．