题目内容

19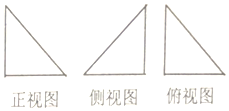．一几何体的三视图如图所示，三个三角形都是直角边为2的等腰直角三角形，该几何体的顶点都在球O上，球O的表面积为（　　）
A．16πB．3πC．$4\sqrt{3}π$D．12π

分析 由三视图可知：该几何体是一个三棱锥，如图所示，AB=AC=AD=2，且AB，AC，AD两两垂直．把此三棱锥补成正方体，则这个空间几何体的外接球的直径为此正方体的对角线，即可得出．

解答 解：由三视图可知：该几何体是一个三棱锥，如图所示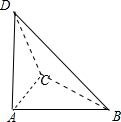，AB=AC=AD=2，且AB，AC，AD两两垂直．
把此三棱锥补成正方体，则这个空间几何体的外接球的直径为此正方体的对角线2$\sqrt{3}$，
因此这个空间几何体的外接球的表面积S=4π•3=12π．
故选：D．

点评 本题考查了三棱锥的三视图、正方体的外接球的表面积计算，考查了计算能力，属于基础题．

练习册系列答案
相关题目
9．（Ⅰ）函数f（x）满足对任意的实数x，y都有f（xy）=f（x）+f（y），且f（4）=2，求f（$\sqrt{2}$）的值；
（Ⅱ）已知函数f（x）是定义在[-1，1]上的奇函数，且f（x）在[-1，1]上递增，求不等式f（x+$\frac{1}{2}$）+f（x-1）＜0
的解集．
10．4个男生4个女生站成一排，要求相邻两人性别不同且男生甲与女生乙相邻，则这样的站法有（　　）
A．576种B．504种C．288种D．252种
7．已知f（x）=x（lnx-mx）（m∈R）．
（I）当m=1时，求f（x）过点（1，-1）的切线方程；
（Ⅱ）若函数F（x）=1nx+$\frac{1}{2}$x2-2mx+1两个极值点x1，x2，且x1＜x2，求证：f（x2）＜-1＜f（x1）
14．将函数$y=sin（x+\frac{π}{3}）$的图象向x轴正方向平移$\frac{π}{6}$个单位后，得到的图象解析式是（　　）
A．$y=sin（x+\frac{π}{6}）$B．$y=sin（x-\frac{π}{6}）$C．$y=sin（x-\frac{2π}{3}）$D．$y=sin（x+\frac{2π}{3}）$
4．已知x，y满足：$\left\{\begin{array}{l}x+y-1≥0\\ 4x-y-9≤0\\ x-4y+9≥0\end{array}\right.$，则z=x-y的最大值为3．
11．如图某几何体的三视图是直角边长为1的三个等腰直角三角形，则该几何体的外接球的表面积为（　　）
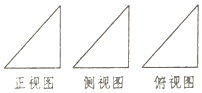
A．$\frac{3}{2}π$B．$\sqrt{3}π$C．$\frac{{\sqrt{3}}}{2}π$D．3π
8．设全集U={（x，y）|x，y∈R}，集合M={（x，y）|$\frac{y-3}{x-2}$=1}，N={（x，y）|y=x+1}，则N∩（∁UM）等于（　　）
A．∅B．{（2，3）}C．（2，3）D．{（x，y）|y=x+1}
9．函数f（x）=x3+4x+9的图象在x=1处的切线在x轴上的截距为（　　）
A．7B．1C．-1D．-7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网