题目内容
9.(Ⅰ)函数f(x)满足对任意的实数x,y都有f(xy)=f(x)+f(y),且f(4)=2,求f($\sqrt{2}$)的值;(Ⅱ)已知函数f(x)是定义在[-1,1]上的奇函数,且f(x)在[-1,1]上递增,求不等式f(x+$\frac{1}{2}$)+f(x-1)<0
的解集.
分析 解:(Ⅰ)直接利用赋值法求得
(Ⅱ)由f(x)是[-1,1]上的奇函数得f(x+$\frac{1}{2}$)<f(1-x),又f(x)在[-1,1]上递增$\left\{\begin{array}{l}{-1≤x+\frac{1}{2}≤1}\\{-1≤1-x≤1}\\{x+\frac{1}{2}<1-x}\end{array}\right.$
解答 解:(Ⅰ)f(4)=f(2×2)=f(2)+f(2)=2
∴2f(2)=2⇒f(2)=1
又∵f(2)=f($\sqrt{2}•\sqrt{2}$)=f($\sqrt{2}$)+f($\sqrt{2}$)═
∴2f($\sqrt{2}$)=1⇒f($\sqrt{2}$)=$\frac{1}{2}$
(Ⅱ)由f(x)是[-1,1]上的奇函数得f(x+$\frac{1}{2}$)<f(1-x)
又f(x)在[-1,1]上递增
$\left\{\begin{array}{l}{-1≤x+\frac{1}{2}≤1}\\{-1≤1-x≤1}\\{x+\frac{1}{2}<1-x}\end{array}\right.$解得$0≤x<\frac{1}{4}$
∴不等式解集为[0,$\frac{1}{4}$)
点评 本题考查了抽象函数的赋值法,及抽象函数不等式的解法,属于基础题.

练习册系列答案
相关题目
10.若a、b为实数,则“a<1”是“$\frac{1}{a}>1$”的( )条件.
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分也不必要 |
17.已知函数$f(x)=\frac{{{x^2}-2x}}{x-2},g(x)=\sqrt{1+x}+\sqrt{1-x}$,下列判断正确的是( )
| A. | 函数f(x)是奇函数,函数g(x)是偶函数 | |
| B. | 函数f(x)不是奇函数,函数g(x)是偶函数 | |
| C. | 函数f(x)是奇函数,函数g(x)不是偶函数 | |
| D. | 函数f(x)不是奇函数,函数g(x)不是偶函数 |
1.已知全集U={1,2,3,4,5},集合A={1,2,3},B={2,4},则(∁UA)∪B为( )
| A. | {4} | B. | {2,4,5} | C. | {1,2,3,4} | D. | {1,2,4,5} |
18.设等差数列{an}的前n项和为Sn,且S6=3,S9=45,则S3=( )
| A. | 39 | B. | -39 | C. | 12 | D. | -12 |
19.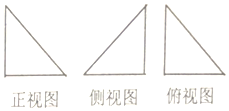 一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )
一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )
 一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )
一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )| A. | 16π | B. | 3π | C. | $4\sqrt{3}π$ | D. | 12π |