题目内容
8.设全集U={(x,y)|x,y∈R},集合M={(x,y)|$\frac{y-3}{x-2}$=1},N={(x,y)|y=x+1},则N∩(∁UM)等于( )| A. | ∅ | B. | {(2,3)} | C. | (2,3) | D. | {(x,y)|y=x+1} |
分析 由全集U及M,求出M的补集,找出N与M补集的交集即可.
解答 解:集合M={(x,y)|$\frac{y-3}{x-2}$=1}={(x,y)|y=x+1,x≠2},
则(∁UM)表示点除了点(2,3),其余的点不在直线y=x+1上,
∴则N∩(∁UM)={(2,3)},
故选:B
点评 此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.设等差数列{an}的前n项和为Sn,且S6=3,S9=45,则S3=( )
| A. | 39 | B. | -39 | C. | 12 | D. | -12 |
19.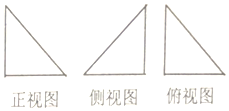 一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )
一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )
 一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )
一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )| A. | 16π | B. | 3π | C. | $4\sqrt{3}π$ | D. | 12π |
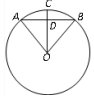 如图,⊙O的半径为10,弦AB的长为12,OD⊥AB,交AB于点D,交⊙O于点C,则OD=8,CD=2.
如图,⊙O的半径为10,弦AB的长为12,OD⊥AB,交AB于点D,交⊙O于点C,则OD=8,CD=2.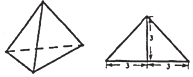 已知一个正三棱锥的正视图为等腰直角三角形,其尺寸如图所示,则此正三棱锥的体积9$\sqrt{3}$,其侧视图的周长为$5\sqrt{3}+\sqrt{21}$.
已知一个正三棱锥的正视图为等腰直角三角形,其尺寸如图所示,则此正三棱锥的体积9$\sqrt{3}$,其侧视图的周长为$5\sqrt{3}+\sqrt{21}$.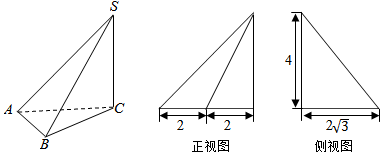
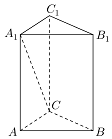 如图,已知正三棱柱ABC-A1B1C1的底面积为$\frac{{9\sqrt{3}}}{4}$,侧面积为36;
如图,已知正三棱柱ABC-A1B1C1的底面积为$\frac{{9\sqrt{3}}}{4}$,侧面积为36;