题目内容
 如图三棱柱ABC-A1B1C1的底面是边长为3的正三角形,侧棱AA1垂直于底面ABC1;AA1=
如图三棱柱ABC-A1B1C1的底面是边长为3的正三角形,侧棱AA1垂直于底面ABC1;AA1=3
| ||
| 2 |
(1)求证:直线BC1∥平面AB1D
(2)若在几何体A1B1C1-ACD内随机取一点,求该点落在三棱锥C1-ABB1内的概率.
考点:直线与平面平行的判定,几何概型
专题:概率与统计
分析:(1)根据线面平行的判定定理即可得到结论.
(2)求出对于几何体的体积,利用几何槪型的概率公式即可得到结论.
(2)求出对于几何体的体积,利用几何槪型的概率公式即可得到结论.
解答:
解:(1)由三棱柱ABC-A1B1C1可知,BC∥B1C1,BC=B1C1,
D是CB延长线上一点,且BD=BC,
则BD∥B1C1,BD=B1C1,
即四边形BDB1C1为平行四边形,
故BC1∥DB1,
又DB1?平面AB1D,BC?AB1D,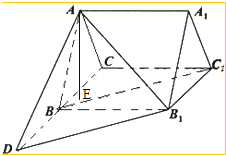
故BC1∥平面AB1D.
(2)由A向BC作垂线,垂足为E,
则AE⊥BC,
又AA1⊥底面ABC,且AA1∥CC1,
故CC1⊥底面ABC,
则CC1⊥AE,
故点A到平面BB1C1的距离为AE,
∵底面ABC是边长为3的正三角形,
∴AE=
,
则三棱锥C1-ABB1内体积V=
|AE|•S=
×
×(
×3×
)=
,
三棱柱A1B1C1-ACD的体积为
×
×
×3=
,
故所求的概率P=
=
.
D是CB延长线上一点,且BD=BC,
则BD∥B1C1,BD=B1C1,
即四边形BDB1C1为平行四边形,
故BC1∥DB1,
又DB1?平面AB1D,BC?AB1D,

故BC1∥平面AB1D.
(2)由A向BC作垂线,垂足为E,
则AE⊥BC,
又AA1⊥底面ABC,且AA1∥CC1,
故CC1⊥底面ABC,
则CC1⊥AE,
故点A到平面BB1C1的距离为AE,
∵底面ABC是边长为3的正三角形,
∴AE=
3
| ||
| 2 |
则三棱锥C1-ABB1内体积V=
| 1 |
| 3 |
| 1 |
| 3 |
3
| ||
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
| 27 |
| 8 |
三棱柱A1B1C1-ACD的体积为
| 4 |
| 3 |
3
| ||
| 2 |
| ||
| 4 |
| 27 |
| 2 |
故所求的概率P=
| ||
|
| 1 |
| 4 |
点评:本题主要考查线面平行的判定以及,几何槪型的概率的计算,综合性较强.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
若某程序框图如图所示,则该程序运行后输出的值是( )


| A、4 | B、5 | C、6 | D、7 |
已知实数x,y满足
,则z=x+2y的最大值为( )
|
| A、-3 | B、21 | C、3 | D、24 |
 随机抽取100名高三学生的2014年省质检数学成绩,经数据处理后制作如图所示的频率分布直方图,那么,根据图形信息,可以推断出成绩在(80,100)之间的人数是( )
随机抽取100名高三学生的2014年省质检数学成绩,经数据处理后制作如图所示的频率分布直方图,那么,根据图形信息,可以推断出成绩在(80,100)之间的人数是( ) 如图,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F.求证:△DEF∽△EAF.
如图,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F.求证:△DEF∽△EAF.