题目内容
某儿童玩具自动售货机里共有18只“海宝”和2只“熊猫”，而在每投一枚一元硬币后，从出口随机掉出一个玩具，则某孩子投了两次硬币，两次都买到的是“海宝”的概率是 ．（结果用最简分数表示）
考点：等可能事件的概率
专题：计算题
分析：本题是一个等可能事件的概率，试验发生所包含的事件是从20只玩具中抽个，共有C202种结果，满足条件的事件是得到两只海宝，共有C182，得到概率．
解答：
解：由题意知本题是一个等可能事件的概率，
试验发生所包含的事件是从20只玩具中抽个，共有C202=190种结果，
满足条件的事件是得到两只海宝，共有C182=153，
∴某孩子投了两次硬币，两次都买到的是“海宝”的概率是
故答案为：
试验发生所包含的事件是从20只玩具中抽个，共有C202=190种结果，
满足条件的事件是得到两只海宝，共有C182=153，
∴某孩子投了两次硬币，两次都买到的是“海宝”的概率是
| 153 |
| 190 |
故答案为：
| 153 |
| 190 |
点评：本题看出等可能事件的概率，本题解题的关键是利用组合数表示出所有事件数和满足条件的事件数，本题是一个基础题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知实数k满足
＞1．则方程x2-kx+1=0的两个根可分别作为（ ）
| 1 |
| k-2 |
| A、一椭圆和一双曲线的离心率 |
| B、两抛物线的离心率 |
| C、一椭圆和一抛物线的离心率 |
| D、两椭圆的离心率 |
设f（x）是定义域为R的奇函数，且在（0，+∞）上是减函数，若f（1）=0，则不等式f（x）＞0的解集是（ ）
| A、（-∞，-1）∪（1，+∞） |
| B、（-1，0）∪（0，1） |
| C、（-∞，-1）∪（0，1） |
| D、（-1，0）∪（1，+∞） |
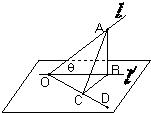如图，l是平面α的斜线，斜足是O，A是l上任意一点，AB是平面α的垂线，B是垂足，设OD是平面α内与OB不同的一条直线，AC垂直于OD于C，若直线l与平面α所成的角θ=45°，∠BOC=45°，求∠AOC的大小．