题目内容
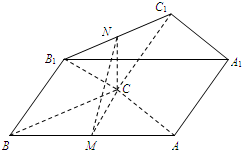 如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点.
如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点.(1)求证:MN∥平面AA1C1C;
(2)若CC1=CB1,CA=CB,平面CC1B1B⊥平面ABC,求证:AB⊥平面CMN.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)取A1C1的中点P,连接AP,NP.证得四边形AMNP为平行四边形.再由线面平行的判定定理即可得到;
(2)运用面面垂直的性质定理和线面垂直的性质和判定定理,即可得证.
(2)运用面面垂直的性质定理和线面垂直的性质和判定定理,即可得证.
解答:
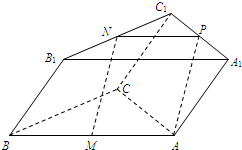 证明:(1)取A1C1的中点P,连接AP,NP.
证明:(1)取A1C1的中点P,连接AP,NP.
因为C1N=NB1,C1P=PA1,所以NP∥A1B1,NP=
A1B1.
在三棱柱ABC-A1B1C1中,A1B1∥AB,A1B1=AB.
故NP∥AB,且NP=
AB.
因为M为AB的中点,所以AM=
AB.
所以NP=AM,且NP∥AM.
所以四边形AMNP为平行四边形.
所以MN∥AP.
因为AP?平面AA1C1C,MN?平面AA1C1C,
所以MN∥平面AA1C1C.
(2)因为CA=CB,M为AB的中点,所以CM⊥AB.
因为CC1=CB1,N为B1C1的中点,所以CN⊥B1C1.
在三棱柱ABC-A1B1C1中,BC∥B1C1,所以CN⊥BC.
因为平面CC1B1B⊥平面ABC,平面CC1B1B∩平面ABC=BC.CN?平面CC1B1B,
所以CN⊥平面ABC.
因为AB?平面ABC,所以CN⊥AB.
因为CM?平面CMN,CN?平面CMN,CM∩CN=C,
所以AB⊥平面CMN.
 证明:(1)取A1C1的中点P,连接AP,NP.
证明:(1)取A1C1的中点P,连接AP,NP.因为C1N=NB1,C1P=PA1,所以NP∥A1B1,NP=
| 1 |
| 2 |
在三棱柱ABC-A1B1C1中,A1B1∥AB,A1B1=AB.
故NP∥AB,且NP=
| 1 |
| 2 |
因为M为AB的中点,所以AM=
| 1 |
| 2 |
所以NP=AM,且NP∥AM.
所以四边形AMNP为平行四边形.
所以MN∥AP.
因为AP?平面AA1C1C,MN?平面AA1C1C,
所以MN∥平面AA1C1C.
(2)因为CA=CB,M为AB的中点,所以CM⊥AB.
因为CC1=CB1,N为B1C1的中点,所以CN⊥B1C1.
在三棱柱ABC-A1B1C1中,BC∥B1C1,所以CN⊥BC.
因为平面CC1B1B⊥平面ABC,平面CC1B1B∩平面ABC=BC.CN?平面CC1B1B,
所以CN⊥平面ABC.
因为AB?平面ABC,所以CN⊥AB.
因为CM?平面CMN,CN?平面CMN,CM∩CN=C,
所以AB⊥平面CMN.
点评:本题考查线面平行的判定定理和线面、面面垂直的判定和性质定理,考查逻辑推理能力,注意定理的条件的全面性,属于基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=(c)=0,现给出如下结论:
①f(0)=f(3);
②f(0)f(1)<0;
③f(1)f(3)<0;
④a2+b2+c2=18.
其中正确结论个数为( )
①f(0)=f(3);
②f(0)f(1)<0;
③f(1)f(3)<0;
④a2+b2+c2=18.
其中正确结论个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知双曲线
-
=1的右焦点为(3,0),则a的值等于( )
| x2 |
| a2 |
| y2 |
| 5 |
| A、2 | ||
| B、3 | ||
| C、4 | ||
D、
|
若A={(2,-2),(2,2)},则集合A中元素的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
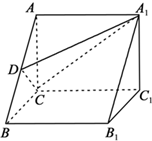 如图,在三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1=2,D为AB的中点,且CD⊥DA1.
如图,在三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1=2,D为AB的中点,且CD⊥DA1.