题目内容
18.已知$tanθ=\frac{1}{3}$,则$sin({\frac{3}{2}π+2θ})$的值为( )| A. | $-\frac{4}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{5}$ |
分析 由已知利用诱导公式,二倍角的余弦函数公式,同角三角函数基本关系式化简所求即可计算得解.
解答 解:∵tanθ=$\frac{1}{3}$,
∴$sin({\frac{3}{2}π+2θ})$=-cos2θ=$\frac{si{n}^{2}θ-co{s}^{2}θ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{ta{n}^{2}θ-1}{ta{n}^{2}θ+1}$=$\frac{\frac{1}{9}-1}{\frac{1}{9}+1}$=-$\frac{4}{5}$.
故选:A.
点评 本题主要考查了诱导公式,二倍角的余弦函数公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
9.设全集U=R,集合A={x|x-1≤1},集合B={y|y=2x,x<1},则A∩(∁UB)=( )
| A. | {x|0<x<2} | B. | ∅ | C. | {0,2} | D. | {x|x≤0或x=2} |
8.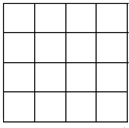 将“丹、东、市”填入如图所示的4×4小方格内,每格内只填入一个汉字,且任意两个汉字既不同行也不同列,则不同的填写方法有( )
将“丹、东、市”填入如图所示的4×4小方格内,每格内只填入一个汉字,且任意两个汉字既不同行也不同列,则不同的填写方法有( )
 将“丹、东、市”填入如图所示的4×4小方格内,每格内只填入一个汉字,且任意两个汉字既不同行也不同列,则不同的填写方法有( )
将“丹、东、市”填入如图所示的4×4小方格内,每格内只填入一个汉字,且任意两个汉字既不同行也不同列,则不同的填写方法有( )| A. | 288 | B. | 144 | C. | 576 | D. | 96 |