题目内容
已知三棱锥P-ABC，PA⊥AB，PA⊥AC，∠BAC=120°，PA=AB=AC=2，则三棱锥的外接球体积为 ．
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：求出△ABC的外接圆的半径，三棱锥的外接球的半径，即可求出三棱锥的外接球体积．
解答：
解：设△ABC的外接圆的半径为r，三棱锥的外接球的半径为R，则
∵AB=AC=2，∠BAC=120°，
∴BC=
=2
，
∴2r=
=4，
∴4R2=16+4，
∴R=
，
∴三棱锥的外接球体积为
π•(
)3=
π，
故答案为：
π．
∵AB=AC=2，∠BAC=120°，
∴BC=
4+4-2×2×2×(-
|
| 3 |
∴2r=
2
| ||||
|
∴4R2=16+4，
∴R=
| 5 |
∴三棱锥的外接球体积为
| 4 |
| 3 |
| 5 |
20
| ||
| 3 |
故答案为：
20
| ||
| 3 |
点评：本题考查三棱锥的外接球体积，考查学生的计算能力，确定三棱锥的外接球的半径是关键
练习册系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
cos
-tan
+
tan2
+sin
+cos2
+sin
的值等于（ ）
| π |
| 3 |
| 5π |
| 4 |
| 3 |
| 4 |
| π |
| 6 |
| 11π |
| 6 |
| 7π |
| 6 |
| 3π |
| 2 |
| A、-1 | ||
| B、0 | ||
| C、1 | ||
D、-
|
已知约束条件
，且目标函数z=x-2y的最大值是4，则z的最小值是（ ）
|
| A、-2 | B、-7 | C、-3 | D、-5 |
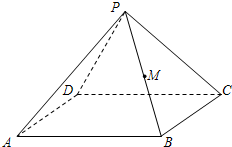四棱锥P-ABCD中，棱长PD=a，底面ABCD是边长为a的菱形，点M为PB中点