��Ŀ����
14���躯��f��x����g��x���Ķ�����ֱ�ΪA��B����A⊆B������������x��A������g��x��=f��x�������g��x������Ϊf��x����B�ϵ�һ�����غ�������f��x��=e-x��x-1����x��0����g��x��Ϊf��x����R�ϵ�һ�����غ�������g��x�����溯���������������⣺�ٵ�x��0ʱ��g��x��=e-x��1-x����
�ں���g��x����3����㣻
��g��x����0�Ľ⼯Ϊ��-1��0���ȣ�1��+�ޣ���
��?x1��x2��R������$|g��{x_1}��-g��{x_2}��|��\frac{2}{e^2}$��
������ȷ����ĸ����ǣ�������
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
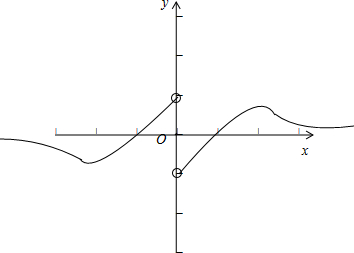
���� ��x��0����-x��0���ɺ��������ʿɵý���ʽ�����Тٵ���٣�������������ͼ��ɶ��������������жϣ�
���  �⣺������ã�x��0ʱ��g��x��=f��x��=e-x��x-1����
�⣺������ã�x��0ʱ��g��x��=f��x��=e-x��x-1����
��x��0ʱ����-x��0��g��-x��=f��-x��=ex��-x-1��=-g��x��������g��x��=ex��x+1�����ʢٲ���ȷ��
��x��0ʱ�Ľ���ʽ�����ɵã�g�䣨x��=ex��x+2�����������0�����x=-2��
�ҵ�x�ʣ�-�ޣ�-2���ϵ���С��0�����������ݼ�����x�ʣ�-2��+�ޣ��ϵ�������0����������������
x=-2��Ϊ��Сֵ�㣬��g��-2����-1������x=1������ֵΪ0���ҵ�x��-1�Ǻ���ֵΪ����
����Ϊ�溯����ͼ�����ԭ�����ĶԳƣ��ʺ���f��x����ͼ��Ӧ��ͼ��ʾ��
��ͼ���֪������f��x����3����㣬�ʢڢ���ȷ��
���ں���-1��g��x����1�����ж�?x1��x2��R��|g��x2��-g��x1��|��2����������ܲ���ȷ��
��ѡ��B��
���� �����Ǹ��¶����⣬��Ҫ�������ú�����ż����������ʽ�ķ������ڽ���ʱע������¶�������⣮����������ͼ���ǽ������Ĺؼ��������е��⣮

��ϰ��ϵ�д�
 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
�����Ŀ
9������ѧ���ɷ�֤������ʽ$1+\frac{1}{2}+\frac{1}{3}+��+\frac{1}{{{2^n}-1}}��n��n��{N^*}��n��2��$������֤n=n0��n0Ϊ��ʼֵ��ʱ������ʽ���Ϊ��������
| A�� | 1 | B�� | $1+\frac{1}{2}$ | ||
| C�� | $1+\frac{1}{2}+\frac{1}{3}$ | D�� | $1+\frac{1}{2}+\frac{1}{3}+��+\frac{1}{{{2^{n_0}}-1}}$ |
6�����к����У���ż�����������䣨0��1���ϵ�������Ϊ���ǣ�������
| A�� | y=ln��x+1�� | B�� | y=$\frac{1}{2}$x2+cosx | C�� | y=x4-3x2 | D�� | y=3x+sinx |
3��������R�ϵĺ���f��x������f��x+6��=f��x������-3��x��-1ʱ��f��x��=-��x+2��2����-1��x��3ʱ��f��x��=x����f��1��+f��2��+f��3��+��+f��2017��=��������
| A�� | 337 | B�� | 338 | C�� | 1678 | D�� | 2012 |
4����֪f��x���Ƕ�����R�ϵ�ż��������[0��+�ޣ���������������a=f��sin$\frac{12��}{7}$����b=f��cos$\frac{5��}{7}$����c=f��tan$\frac{2��}{7}$����������
| A�� | a��b��c | B�� | c��a��b | C�� | b��a��c | D�� | c��b��a |
 Ϊ�˲�����ɽ��M��N��ľ��룬�ɻ���ˮƽ������A��B������в�����A��B��M��N��ͬһ��Ǧ��ƽ���ڣ���ʾ��ͼ�����ɻ��ܹ������������и��Ǻ�A��B��ľ��룮�ֲ��AB��ľ���Ϊd��A�㵽M��N��ĸ���Ϊ��1����1��B�㵽M��N��ĸ���Ϊ��2����2���뽫�������õ���������ͼ�ϱ������������õ����ݡ���ʽ�ͱ�Ҫ������д��M��N�����ı���ʽ����������õ�����д��MN�ı���ʽ����
Ϊ�˲�����ɽ��M��N��ľ��룬�ɻ���ˮƽ������A��B������в�����A��B��M��N��ͬһ��Ǧ��ƽ���ڣ���ʾ��ͼ�����ɻ��ܹ������������и��Ǻ�A��B��ľ��룮�ֲ��AB��ľ���Ϊd��A�㵽M��N��ĸ���Ϊ��1����1��B�㵽M��N��ĸ���Ϊ��2����2���뽫�������õ���������ͼ�ϱ������������õ����ݡ���ʽ�ͱ�Ҫ������д��M��N�����ı���ʽ����������õ�����д��MN�ı���ʽ����