��Ŀ����
4�� Ϊ�˲�����ɽ��M��N��ľ��룬�ɻ���ˮƽ������A��B������в�����A��B��M��N��ͬһ��Ǧ��ƽ���ڣ���ʾ��ͼ�����ɻ��ܹ������������и��Ǻ�A��B��ľ��룮�ֲ��AB��ľ���Ϊd��A�㵽M��N��ĸ���Ϊ��1����1��B�㵽M��N��ĸ���Ϊ��2����2���뽫�������õ���������ͼ�ϱ������������õ����ݡ���ʽ�ͱ�Ҫ������д��M��N�����ı���ʽ����������õ�����д��MN�ı���ʽ����
Ϊ�˲�����ɽ��M��N��ľ��룬�ɻ���ˮƽ������A��B������в�����A��B��M��N��ͬһ��Ǧ��ƽ���ڣ���ʾ��ͼ�����ɻ��ܹ������������и��Ǻ�A��B��ľ��룮�ֲ��AB��ľ���Ϊd��A�㵽M��N��ĸ���Ϊ��1����1��B�㵽M��N��ĸ���Ϊ��2����2���뽫�������õ���������ͼ�ϱ������������õ����ݡ���ʽ�ͱ�Ҫ������д��M��N�����ı���ʽ����������õ�����д��MN�ı���ʽ����
���� �ڡ�ABM�͡�ABN���������Ҷ�������BM��BN���ڡ�BMN���������Ҷ�������MN��
��� 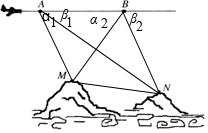 �⣺�������֪��BAM=��1����ABM=��2��AB=d��
�⣺�������֪��BAM=��1����ABM=��2��AB=d��
���ABM����AMB=180��-��1-��2��
�����Ҷ����ɵ�$\frac{AB}{sin��AMB}=\frac{BM}{sin��BAM}$����$\frac{d}{sin��{��}_{1}+{��}_{2}��}$=$\frac{BM}{sin{��}_{1}}$��
��BM=$\frac{dsin{��}_{1}}{sin��{��}_{1}+{��}_{2}��}$��
�ڡ�ABN�У���ANB=��2-��1��
�����Ҷ�����$\frac{BN}{sin��BAN}=\frac{AB}{sin��ANB}$����$\frac{d}{sin��{��}_{2}-{��}_{1}��}$=$\frac{BN}{sin{��}_{1}}$��
��BN=$\frac{dsin{��}_{1}}{sin��{��}_{2}-{��}_{1}��}$��
�ڡ�BMN�У���MBN=180��-��2-��2����cos��MBN=-cos����2+��2����
�����Ҷ�����MN2=BM2+BN2-2BM•BN•cos��MBN=$\frac{{d}^{2}si{n}^{2}{��}_{1}}{si{n}^{2}��{��}_{1}+{��}_{2}��}$+$\frac{{d}^{2}si{n}^{2}{��}_{1}}{si{n}^{2}��{��}_{2}-{��}_{1}��}$+$\frac{{2d}^{2}sin{��}_{1}sin{��}_{1}cos��{��}_{2}+{��}_{2}��}{sin��{��}_{1}+{��}_{2}��sin��{��}_{2}-{��}_{1}��}$��
��MN=d$\sqrt{\frac{si{n}^{2}{��}_{1}}{si{n}^{2}��{��}_{1}+{��}_{2}��}+\frac{si{n}^{2}{��}_{1}}{si{n}^{2}��{��}_{2}-{��}_{1}��}+\frac{2sin{��}_{1}sin{��}_{1}cos��{��}_{2}+{��}_{2}��}{sin��{��}_{1}+{��}_{2}��sin��{��}_{2}-{��}_{1}��}}$��
���� ���⿼���������Ҷ����ڽ��������е�Ӧ�ã������е��⣮

| A�� | 3125 | B�� | 5625 | C�� | 8125 | D�� | 0625 |
| A�� | 19 | B�� | 20 | C�� | 21 | D�� | 22 |
 ����ͼ�����ͼ���㣺���������3�β�ֹͣ���������x��ȡֵ��Χ�ǣ�������
����ͼ�����ͼ���㣺���������3�β�ֹͣ���������x��ȡֵ��Χ�ǣ�������| A�� | ��10��28] | B�� | ��10��28�� | C�� | [10��28�� | D�� | [10��28] |
 ij����������ͼ��ͼ��ʾ�����и���ͼ��һ������ֱ�������Σ���������������ı����Ϊ��������
ij����������ͼ��ͼ��ʾ�����и���ͼ��һ������ֱ�������Σ���������������ı����Ϊ��������| A�� | 5�� | B�� | $\sqrt{5}$�� | C�� | $\frac{5��}{3}$ | D�� | $\frac{{5\sqrt{5}��}}{6}$ |
| A�� | P��3��=3 | B�� | P��5��=1 | C�� | P��2003����P��2005�� | D�� | P��2008����P��2010�� |
| A�� | 2 | B�� | $\frac{1}{2}$ | C�� | $\sqrt{3}$ | D�� | $\frac{{\sqrt{3}}}{3}$ |