题目内容
8.在直角坐标系中,定义两点A(x1,y1),B(x2,y2)之间的“直角距离”为d(A,B)=|x1-x2|+|y1-y2|.现有以下命题:
①若A,B是x轴上两点,则d(A,B)=|x1-x2|;
②已知点A(1,2),点B(cos2θ,sin2θ),则d(A,B)为定值;
③已知点A(2,1),点B在圆x2+y2=1上,则d(A,B)的取值范围是(3-$\sqrt{2}$,3+$\sqrt{2}$);
④若|AB|表示A,B两点间的距离,那么|AB|≥$\frac{\sqrt{2}}{2}$d(A,B).
其中真命题的是①②④(写出所有真命题的序号)
分析 根据距离公式判断①④,根据三角函数的性质判断②③.
解答 解:①当A,B是x轴上两点时,y1=y2=0,d(A,B)=|x1-x2|显然成立,∴①对;
②由x∈[0,1]得,d(A,B)=|1-cos2θ|+|2-sin2θ|=1-cos2θ+2-sin2θ=2为定值,∴②对;
③由条件得$d(A,B)=|{2-cosθ}|+|{1-sinθ}|=3-\sqrt{2}sin(θ+\frac{π}{4})$,
∴$d(A,B)∈[{3-\sqrt{2},3+\sqrt{2}}]$,∴③不对;
④由条件知${|{AB}|^2}=({x_1}-{x_2}{)^2}+{({y_1}-{y_2})^2}≥\frac{1}{2}{(|{{x_1}-{x_2}}|+|{{y_1}-{y_2}}|)^2}$,
∴$|{AB}|=≥\frac{{\sqrt{2}}}{2}(|{{x_1}-{x_2}}|+|{{y_1}-{y_2}}|)=\frac{{\sqrt{2}}}{2}d(A,B)$,∴④对;
故答案为:①②④.
点评 本题考查了两点间距离公式的应用,考查三角函数问题,是一道中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
19.已知sin(α+$\frac{π}{3}$)=$\frac{1}{3}$,且α为三角形一内角,则cos(α+$\frac{π}{6}$)的值等于$\frac{-2\sqrt{6}+1}{6}$.
3.sin15°sin75°=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
18.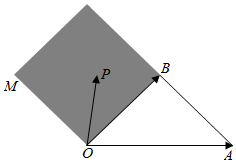 如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则实数对(x,y)可以是( )
如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则实数对(x,y)可以是( )
 如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则实数对(x,y)可以是( )
如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则实数对(x,y)可以是( )| A. | ($\frac{1}{4}$,$\frac{3}{4}$) | B. | (-$\frac{2}{3}$,$\frac{2}{3}$) | C. | (-$\frac{1}{4}$,$\frac{3}{4}$) | D. | (-$\frac{1}{5}$,$\frac{7}{5}$) |
 如图,圆中有一内接等腰三角形,且三角形底边经过圆心,假设在图中随机撒一把黄豆,则它落在阴影部分的概率为$\frac{1}{π}$.
如图,圆中有一内接等腰三角形,且三角形底边经过圆心,假设在图中随机撒一把黄豆,则它落在阴影部分的概率为$\frac{1}{π}$.