题目内容
8.(1)已知x${\;}^{\frac{1}{4}}$+x${\;}^{-\frac{1}{4}}$=2,求x+x-1的值;(2)计算:($\frac{1}{16}$)${\;}^{-\frac{1}{4}}$-3${\;}^{lo{g}_{3}2}$(log34)•(log827)+2log12$\sqrt{3}$+log${\;}_{\frac{1}{12}}$$\frac{1}{4}$的值.
分析 (1)根据指数幂的运算性质计算即可,
(2)根据指数幂和对数的运算性质计算即可.
解答 解:(1)∵x${\;}^{\frac{1}{4}}$+x${\;}^{-\frac{1}{4}}$=2,
(x${\;}^{\frac{1}{4}}$+x${\;}^{-\frac{1}{4}}$)2=22,
∴${x}^{\frac{1}{2}}+{x}^{-\frac{1}{2}}$=2,
∴(${x}^{\frac{1}{2}}+{x}^{-\frac{1}{2}}$)2=4,
∴x+x-1=2
(2)原式=($\frac{1}{2}$)${\;}^{4×(-\frac{1}{4})}$-2•$\frac{2lg2}{lg3}$•$\frac{3lg3}{3lg2}$+log123+log124=2-4+1=-1
点评 本题考查了指数幂和对数的运算性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.曲线y=$\frac{x}{2x-1}$在点(1,1)处的切线方程为( )
| A. | x-y-2=0 | B. | x+y-2=0 | C. | x+4y-5=0 | D. | x-4y-5=0 |
17.△ABC中,若a=1,b=2,sinA=$\frac{1}{3}$,则sinB=( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{\sqrt{2}}{6}$ |
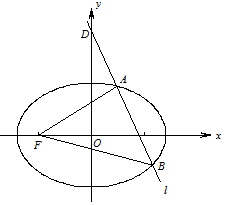 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,短轴端点与椭圆的两个焦点所构成的三角形面积为1,过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,短轴端点与椭圆的两个焦点所构成的三角形面积为1,过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.