题目内容

14．从甲、乙等5名学生中随机选出2人，则甲被选中的概率为（　　）
A．$\frac{1}{5}$B．$\frac{2}{5}$C．$\frac{8}{25}$D．$\frac{9}{25}$

分析 从甲、乙等5名学生中随机选出2人，先求出基本事件总数，再求出甲被选中包含的基本事件的个数，同此能求出甲被选中的概率．

解答 解：从甲、乙等5名学生中随机选出2人，
基本事件总数n=${C}_{5}^{2}$=10，
甲被选中包含的基本事件的个数m=${C}_{1}^{1}{C}_{4}^{1}$=4，
∴甲被选中的概率p=$\frac{m}{n}$=$\frac{4}{10}$=$\frac{2}{5}$．
故选：B．

点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．

练习册系列答案
相关题目
4．已知a、b、c分别为△ABC的三个内角A、B、C的对边，2sinAcos2$\frac{C}{2}$+2sinC•cos2$\frac{A}{2}$=3sinB
（1）证明a、b、c成等差数列；
（2）若∠B为锐角，且a=btanA，求a：b：c的值．
5．设f（x）=sin（2x+$\frac{π}{6}$）+$\frac{1}{2}$，已知f（α）=$\frac{5}{6}$，且α∈（0，$\frac{π}{6}$），求sin2α．
2．已知集合A={1，2，3}，B={x|x2＜9}，则A∩B=（　　）
A．{-2，-1，0，1，2，3}B．{-2，-1，0，1，2}C．{1，2，3}D．{1，2}
9．若x，y满足$\left\{\begin{array}{l}{2x-y≤0}\\{x+y≤3}\\{x≥0}\end{array}\right.$，则2x+y的最大值为（　　）
A．0B．3C．4D．5
4．函数F（x）=ex-1，G（x）=ax2+bx，其中a，b∈R，e是自然对数的底数．
（Ⅰ）若a=0时，y=G（x）为曲线y=F（x）的切线，求b的值；
（Ⅱ）若f（x）=F（x）-G（x），f（1）=0．证明：当e-2＜a＜1时，函数f（x）在区间（0，1）内有零点．
11．集合A={x∈N|x2-2x-3＜0}，B={1，x2}，若A∪B={0，1，2}，则这样的实数x的个数为（　　）
A．1个B．2个C．4个D．3个
8．在平面直角坐标系xoOy中，以O为极点，x轴的正半轴为极轴的极坐标系中，直线l的极坐标方程为θ=$\frac{π}{4}$（ρ∈R），曲线C的参数方程为$\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}$（θ为参数）．
（1）写出直线l与曲线C的直角坐标方程；
（2）过点M平行于直线l的直线与曲线C交于A、B两点，若|MA|•|MB|=3，求点M轨迹的直角坐标方程．
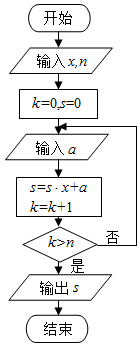9．中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图．执行该程序框图，若输入的x=2，n=2，依次输入的a为2，2，5，则输出的s=（　　）
A．7B．12C．17D．34

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网