题目内容
下列函数中，在其定义域内既是奇函数又是增函数的是（ ）
A、y=
| ||
| B、y=x3 | ||
| C、y=ex | ||
| D、y=lnx |
考点：函数单调性的判断与证明,函数奇偶性的判断
专题：函数的性质及应用
分析：根据反比例函数的单调性，指数函数、对数函数的奇偶性，以及函数单调性的定义即可判断每个函数的奇偶性和单调性，从而找到正确选项．
解答：
解：反比例函数y=
在定义域内没有单调性；
根据奇函数和单调性的定义知y=x3在其定义域内既是奇函数又是增函数；
y=ex在定义域内没奇偶性；
对数函数y=lnx在定义域内没有奇偶性；
∴B正确．
故选B．
| 1 |
| x |
根据奇函数和单调性的定义知y=x3在其定义域内既是奇函数又是增函数；
y=ex在定义域内没奇偶性；
对数函数y=lnx在定义域内没有奇偶性；
∴B正确．
故选B．
点评：考查反比例函数的单调性，奇函数、偶函数的定义，函数单调性的定义，以及指数函数和对数函数的奇偶性．
练习册系列答案
相关题目
已知|
|=6，|
|=8，
•
=22，则|
+
|为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、10 | B、12 | C、72 | D、144 |
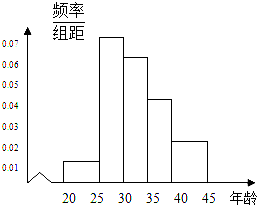南昌市为增强市民的交通安全意识，面向全市征召“小红帽”志愿者在部分交通路口协助交警维持交通，把符合条件的1000名志愿者按年龄分组：第1组[20，25）、第2组[25，30）、第3组[30，35）、第4组[35，40）、第5组[40，45），得到的频率分布直方图如图所示：