题目内容
已知
=(cosα,sinα),
=(cosβ,-sinβ).
(1)若|
+
|=
,求证:
⊥
;
(2)若
=(
,
),
+
=
,求cos(α+β)的值.
| a |
| b |
(1)若|
| a |
| b |
| 2 |
| a |
| b |
(2)若
| c |
| 1 |
| 2 |
| 1 |
| 3 |
| a |
| b |
| c |
考点:平面向量数量积的运算,两角和与差的余弦函数
专题:三角函数的求值,平面向量及应用
分析:(1)运用向量的模的公式和向量的平方即为模的平方,结合向量垂直的条件:数量积为0,即可得证;
(2)首先由向量的加法的运算,再由平方法和同角的平方关系及两角和的余弦公式,计算即可得到.
(2)首先由向量的加法的运算,再由平方法和同角的平方关系及两角和的余弦公式,计算即可得到.
解答:
(1)证明:
=(cosα,sinα),
=(cosβ,-sinβ),
则|
|=
=1,|
|=
=1,
|
+
|=
=
=
,
即有
•
=0,
即
⊥
;
(2)解:若
=(
,
),
+
=
,
则cosα+cosβ=
,sinα-sinβ=
,
两式平方相加可得,
cos2α+sin2α+cos2β+sin2β+2(cosαcosβ-sinαsinβ)=
,
即2+2cos(α+β)=
,
则有cos(α+β)=-
.
| a |
| b |
则|
| a |
| cos2α+sin2α |
| b |
| cos2β+sin2β |
|
| a |
| b |
|
1+1+2
|
| 2 |
即有
| a |
| b |
即
| a |
| b |
(2)解:若
| c |
| 1 |
| 2 |
| 1 |
| 3 |
| a |
| b |
| c |
则cosα+cosβ=
| 1 |
| 2 |
| 1 |
| 3 |
两式平方相加可得,
cos2α+sin2α+cos2β+sin2β+2(cosαcosβ-sinαsinβ)=
| 13 |
| 36 |
即2+2cos(α+β)=
| 13 |
| 36 |
则有cos(α+β)=-
| 59 |
| 72 |
点评:本题主要考查向量的数量积的性质和向量的模的求法,同时考查同角的平方关系及两角和的余弦公式,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
定义运算a?b为执行如图所示的程序框图输出的S值,则(2cos
)?tan
的值为( )
| π |
| 3 |
| 7π |
| 4 |

| A、2 | B、-2 | C、-1 | D、1 |
在棱长为3的正方体内任取一点P,则点P到该正方体的六个面的距离的最小值不大于1的概率为( )
A、
| ||
B、
| ||
C、1-
| ||
D、
|
若集合A={x|-2<x<1},B={x|0<x<2},则集合A∩B=( )
| A、{x|0<x<1} |
| B、{x|-1<x<1} |
| C、{x|-2<x<2} |
| D、{x|1<x<2} |
某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )


| A、90cm3 |
| B、95.5cm3 |
| C、102cm3 |
| D、104cm3 |
下列函数中,在其定义域内既是奇函数又是增函数的是( )
A、y=
| ||
| B、y=x3 | ||
| C、y=ex | ||
| D、y=lnx |
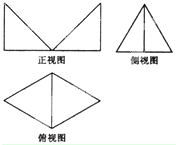 某几何体的三视图如图所示,某正视图是两个全等的三角形,俯视图是一个边长为2的正三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为
某几何体的三视图如图所示,某正视图是两个全等的三角形,俯视图是一个边长为2的正三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为