题目内容
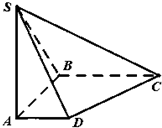 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=2,AD=1.
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=2,AD=1.(1)求证:面SAB⊥面SBC;
(2)求SC与底面ABCD所成角的正切值.
考点:直线与平面所成的角,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)证明SA⊥BC利用AB⊥BC,即可证明BC⊥面SAB,利用平面与平面垂直的判定定理证明面SAB⊥面SBC.
(2)连结AC,说明∠SCA就是SC与底面ABCD所成的角,在直角三角形SCA中,求解即可.
(2)连结AC,说明∠SCA就是SC与底面ABCD所成的角,在直角三角形SCA中,求解即可.
解答:
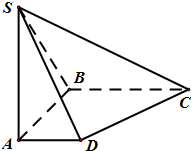 (1)证明:∵SA⊥面ABCD,BC?面ABCD,
(1)证明:∵SA⊥面ABCD,BC?面ABCD,
∴SA⊥BC
又∵AB⊥BC,SA∩AB=A,∴BC⊥面SAB,
∵BC?面SAB,
∴面SAB⊥面SBC…(6分)
(2)解:已知SA⊥面ABCD,连结AC,
则∠SCA就是SC与底面ABCD所成的角,在直角三角形SCA中,SA=2,AC=
=2
,tan∠SCA=
=
=
…(12分)
 (1)证明:∵SA⊥面ABCD,BC?面ABCD,
(1)证明:∵SA⊥面ABCD,BC?面ABCD,∴SA⊥BC
又∵AB⊥BC,SA∩AB=A,∴BC⊥面SAB,
∵BC?面SAB,
∴面SAB⊥面SBC…(6分)
(2)解:已知SA⊥面ABCD,连结AC,
则∠SCA就是SC与底面ABCD所成的角,在直角三角形SCA中,SA=2,AC=
| 22+22 |
| 2 |
| SA |
| AC |
| 2 | ||
2
|
| ||
| 2 |
点评:本题考查直线与平面所成角的求法,平面与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
已知A(-1,3)、B(3,-1),则直线AB的倾斜角为( )
| A、45° | B、60° |
| C、120° | D、135° |
已知
,求z=
的范围( )
|
| 2y+1 |
| x+1 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
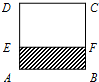 如图E、F是正方形ABCD两边的三等分点,向正方形ABCD内任投一点M,记点M落在阴影区域的概率为p,则a=p是函数y=ax2+2x+1有两个零点的( )
如图E、F是正方形ABCD两边的三等分点,向正方形ABCD内任投一点M,记点M落在阴影区域的概率为p,则a=p是函数y=ax2+2x+1有两个零点的( )| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |