题目内容
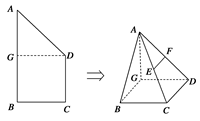
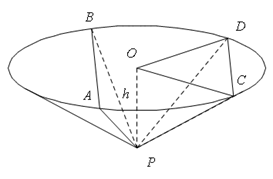
如图1,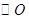 的直径AB=4,点C、D为
的直径AB=4,点C、D为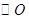 上两点,且
上两点,且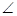 CAB=45°,
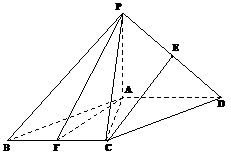
CAB=45°, DAB=60°,F为弧BC的中点.沿直径AB折起,使两个半圆所在平面互相垂直,如图2.
DAB=60°,F为弧BC的中点.沿直径AB折起,使两个半圆所在平面互相垂直,如图2.
(I)求证:OF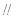 平面ACD;
平面ACD;
(Ⅱ)求二面角C—AD—B的余弦值;
(Ⅲ)在弧BD上是否存在点G,使得FG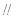 平面ACD?若存在,试指出点G的位置;若不存在,请说明理由.
平面ACD?若存在,试指出点G的位置;若不存在,请说明理由.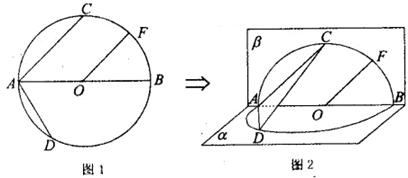
(1)对于线面平行的判定关键是证明 来得到。
来得到。
(2)
(3) 在弧 上存在点
上存在点 ,使得
,使得 //平面
//平面 ,且点
,且点 为弧
为弧 的中点
的中点
解析试题分析:(方法一):证明:(Ⅰ)如右图,连接 ,
, ,
, . …1分 又
. …1分 又 为弧
为弧 的中点,
的中点, ,
, .
. 平面
平面 ,
, 平面
平面 ,
,
 平面
平面 . …4分
. …4分
解:(Ⅱ)过 作
作 于
于 ,连
,连 .
.
 ,平面
,平面 ⊥平面
⊥平面 .
.
 ⊥平面
⊥平面 .又
.又 平面
平面 ,
,  ,
,  平面
平面 ,
, ,则∠
,则∠ 是二面角
是二面角 的平面角.
的平面角. 
 ,
, ,
,  . 由
. 由 ⊥平面
⊥平面 ,
, 平面
平面 ,得
,得 为直角三角形,
为直角三角形,
 ,
,


 =
= =
= . 8分
. 8分
(Ⅲ)取弧 的中点
的中点 ,连结
,连结 、
、 ,则
,则
 …
…
 平面
平面 ,
, 平面
平面 平面
平面
 //平面
//平面 .
.
因此,在弧 上存在点
上存在点 ,使得
,使得 //平面
//平面 ,且点
,且点 为弧
为弧 的中点.…12分
的中点.…12分
(方法二):证明:(Ⅰ)如图,以 所在的直线为
所在的直线为 轴,以
轴,以 所在的直线为
所在的直线为 轴,以
轴,以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系

则

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 中,
中,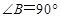 ,
,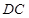 ∥
∥ ,
,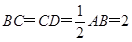 ,
, 为线段
为线段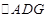 沿
沿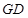 折起,使平面
折起,使平面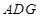 ⊥平面
⊥平面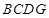 ,得到几何体
,得到几何体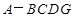 .
.
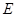 ,
,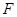 分别为线段
分别为线段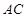 ,
,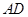 的中点,求证:
的中点,求证: ∥平面
∥平面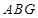 ;
;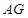 ⊥平面
⊥平面 的值.
的值. .底面圆心为
.底面圆心为 ,其母线与底面所成的角为
,其母线与底面所成的角为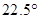 .
.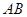 和
和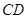 是底面圆
是底面圆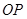 与平面
与平面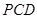 所成的角为
所成的角为 ,
, 
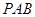 与平面
与平面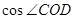 .
.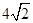 ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。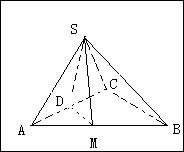
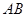 ⊥平面
⊥平面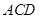 ,
,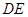 ∥
∥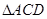 是正三角形,
是正三角形,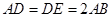 ,且
,且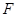 是
是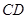 的中点.
的中点.
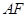 ∥平面
∥平面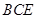 ;
; .
.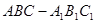 的三视图如图所示,
的三视图如图所示,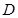 是
是 的中点.
的中点.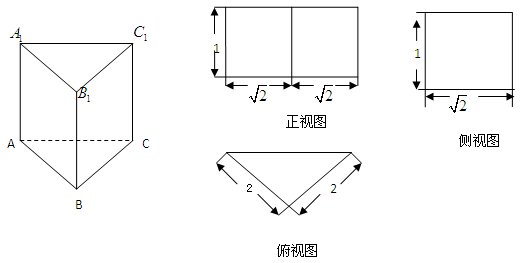
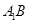 ∥平面
∥平面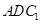 ;
;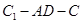 的余弦值;
的余弦值;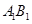 上是否存在点
上是否存在点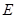 ,使
,使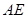 与
与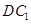 成
成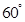 角?若存在,确定
角?若存在,确定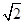 。
。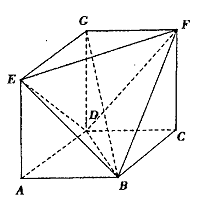
 的值;若不存在,说明理由.
的值;若不存在,说明理由.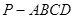 中,
中,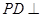 底面
底面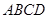 ,面
,面 为侧棱
为侧棱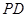 上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
上一点.该四棱锥的俯视图和侧(左)视图如图2所示. 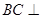 平面
平面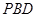 ;
; 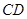 上是否存在点
上是否存在点 ,使
,使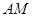 与
与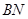 所成角的余弦值为
所成角的余弦值为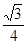 ?若存在,找到所有符合要求的点
?若存在,找到所有符合要求的点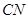 的长;若不存在,说明理由.
的长;若不存在,说明理由.
 ,E、F分别为线段PD和BC的中点.
,E、F分别为线段PD和BC的中点.