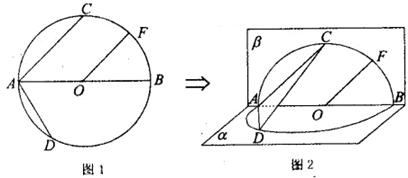
题目内容
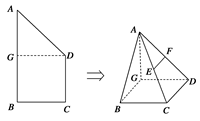
如图,在直角梯形 中,
中,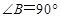 ,
,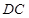 ∥
∥ ,
,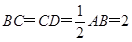 ,
, 为线段
为线段 的中点,将
的中点,将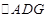 沿
沿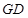 折起,使平面
折起,使平面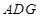 ⊥平面
⊥平面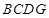 ,得到几何体
,得到几何体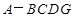 .
.
(1)若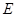 ,
,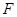 分别为线段
分别为线段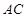 ,
,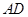 的中点,求证:
的中点,求证: ∥平面
∥平面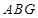 ;
;
(2)求证: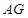 ⊥平面
⊥平面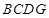 ;
;
(3) 的值.
的值.
(1)主要证明 ∥
∥ (2)主要证明
(2)主要证明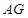 ⊥
⊥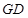 (3)
(3)
解析试题分析:解:(1)证明:依题意,折叠前后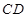 、
、 位置关系不改变,
位置关系不改变,
∴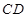 ∥
∥ .
.
∵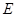 、
、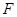 分别为线段
分别为线段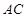 、
、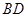 的中点,
的中点,
∴在 中,
中, ∥
∥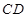 ,∴
,∴ ∥
∥ .
.
又
 平面
平面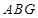 ,
,
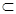 平面
平面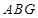 ,
,
∴ ∥平面
∥平面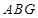 .
.
(2)证明:将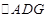 沿
沿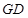 折起后,
折起后,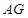 、
、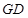 位置关系不改变,
位置关系不改变,
∴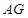 ⊥
⊥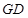 ,
,
又平面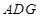 ⊥平面
⊥平面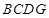 ,平面
,平面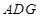
 平面
平面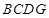 =
=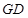 ,
,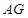
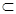 平面
平面 ,
,
∴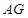 ⊥平面
⊥平面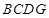 .
.
(3)解:由已知得 ,
,
又由(2)得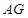 ⊥平面
⊥平面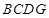 ,即点
,即点 到平面
到平面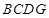 的距离
的距离 ,
,
∴ =
= =
= =
= ×
×
 =
= .
.
考点:平面与平面垂直的性质;棱柱、棱锥、棱台的体积;直线与平面平行的判定.
点评:熟练掌握三角形的中位线定理、线面平行的判定定理及面面、线面垂直的判定和性质定理是解题的关键.

练习册系列答案
相关题目
 ,曲线
,曲线 在
在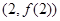 处的切线过点
处的切线过点 .
. 的解析式;
的解析式;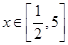 时,求
时,求 中,
中,  是
是 上的点且
上的点且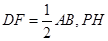 为
为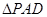 中
中 边上的高.
边上的高. 平面
平面 ;
;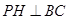 ;
; 上是否存在点
上是否存在点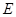 ,使
,使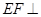 平面
平面 ?说明理由.
?说明理由.
 是正方形,
是正方形,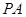 ⊥面
⊥面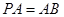 ,
,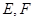 是侧棱
是侧棱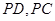 的中点.
的中点.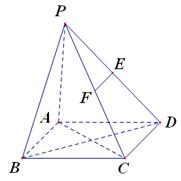
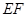 ∥平面
∥平面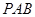 ;
;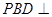 平面
平面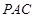 ;
; 与底面
与底面 中,
中,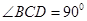 ,
, 平面
平面 ,
,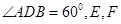 分别是直线
分别是直线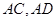 上的点,且
上的点,且

 平面角的余弦值
平面角的余弦值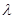 为何值时,平面
为何值时,平面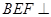 平面
平面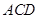
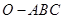 的侧棱
的侧棱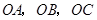 两两垂直,且
两两垂直,且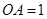 ,
,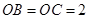 ,
,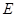 是
是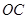 的中点.
的中点.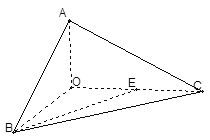
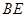 与
与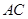 所成的角的余弦值
所成的角的余弦值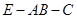 的余弦值
的余弦值 点到面
点到面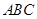 的距离
的距离 是边长为2的正三角形,
是边长为2的正三角形,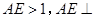 平面ABC,平面
平面ABC,平面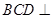 平面ABC,BD=CD,且
平面ABC,BD=CD,且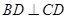 .
.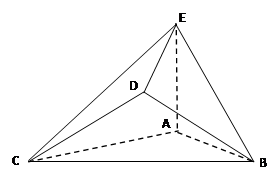
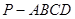 中,底面
中,底面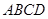 是边长为2的正方形,侧棱
是边长为2的正方形,侧棱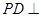 平面
平面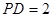 ,
, 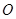 为底面对角线的交点,
为底面对角线的交点, 分别为棱
分别为棱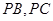 的中点
的中点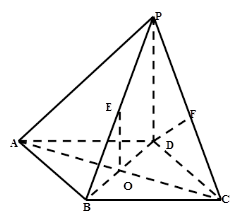
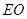 //平面
//平面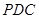 ;
;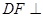 平面
平面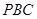 ;
;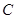 到平面
到平面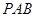 的距离。
的距离。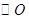 的直径AB=4,点C、D为
的直径AB=4,点C、D为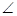 CAB=45°,
CAB=45°,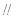 平面ACD;
平面ACD;