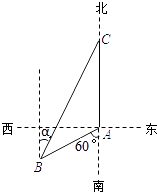
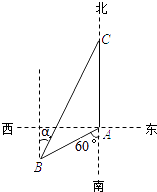
ЬтФПФкШн
ЁОЬтФПЁПЯТБэЬсЙЉСЫФГГЇНкФмНЕКФММЪѕИФдьКѓЩњВњМзВњЦЗЙ§ГЬжаМЧТМЕФВњСПЃЈ![]() ЖжЃЉгыЯргІЕФЩњВњФмКФ
ЖжЃЉгыЯргІЕФЩњВњФмКФ![]() ЃЈЖжЃЉБъзМУКЕФМИзщЖдееЪ§ОнЃК
ЃЈЖжЃЉБъзМУКЕФМИзщЖдееЪ§ОнЃК
|
|
|
|
|
|
|
|
|
|
ЃЈ1ЃЉЧыЛГіЩЯБэЪ§ОнЕФЩЂЕуЭМЃЛВЂжИГі![]() ЪЧЗёЯпадЯрЙиЃЛ
ЪЧЗёЯпадЯрЙиЃЛ
ЃЈ2ЃЉЧыИљОнЩЯБэЬсЙЉЕФЪ§ОнЃЌгУзюаЁЖўГЫЗЈЧѓГі![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬ
ЕФЯпадЛиЙщЗНГЬ![]()
![]() ЃЛ
ЃЛ
ЃЈ3ЃЉвбжЊИУГЇММЪѕИФдьЧА![]() ЖжМзВњЦЗФмКФЮЊ
ЖжМзВњЦЗФмКФЮЊ![]() ЖжБъзМУКЃЌЪдИљОнЧѓГіЕФЯпадЛиЙщЗНГЬЃЌдЄВтЩњВњ
ЖжБъзМУКЃЌЪдИљОнЧѓГіЕФЯпадЛиЙщЗНГЬЃЌдЄВтЩњВњ![]() ЖжМзВњЦЗЕФЩњВњФмКФБШММЪѕИФдьЧАНЕЕЭЖрЩйЖжБъзМУКЃП
ЖжМзВњЦЗЕФЩњВњФмКФБШММЪѕИФдьЧАНЕЕЭЖрЩйЖжБъзМУКЃП
ЃЈВЮПМ:гУзюаЁЖўГЫЗЈЧѓЯпадЛиЙщЗНГЬЯЕЪ§ЙЋЪН ЃЌ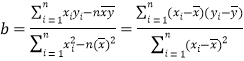 ,
, ![]() .
.
ЁОД№АИЁПЃЈ1ЃЉЩЂЕуЭММћНтЮіЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉАбЫљИјЕФЫФЖдЪ§ОнаДГЩЖдгІЕФЕуЕФзјБъЃЌдкзјБъЯЕжаУшГіРДЃЌЕУЕНЩЂЕуЭМЃЌгЩЭМПЩжЊГі![]() ЪЧЯпадЯрЙиЃЛЃЈ2ЃЉИљОнЫљИјЕФетзщЪ§ОнЧѓГібљБОжааФЕуЕФзјБъЃЌРћгУЙЋЪНЃЌ
ЪЧЯпадЯрЙиЃЛЃЈ2ЃЉИљОнЫљИјЕФетзщЪ§ОнЧѓГібљБОжааФЕуЕФзјБъЃЌРћгУЙЋЪНЃЌ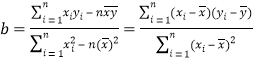 ,ЛиЙщЗНГЬЕФЯЕЪ§ЃЌЕУЕНЯпадЛиЙщЗНГЬЃЛЃЈ3ЃЉИљОнЯпадЛиЙщЗНГЬЃЌМЦЫу
,ЛиЙщЗНГЬЕФЯЕЪ§ЃЌЕУЕНЯпадЛиЙщЗНГЬЃЛЃЈ3ЃЉИљОнЯпадЛиЙщЗНГЬЃЌМЦЫу![]() ЪБЕФЩњВњФмКФЃЌНјЖјПЩЧѓГіБШММИФЧАНЕЕЭЕФБъзМУК.
ЪБЕФЩњВњФмКФЃЌНјЖјПЩЧѓГіБШММИФЧАНЕЕЭЕФБъзМУК.
ЪдЬтНтЮіЃКЃЈ1ЃЉАбЫљИјЕФЫФЖдЪ§ОнаДГЩЖдгІЕФЕуЕФзјБъЃЌдкзјБъЯЕжаУшГіРДЃЌЕУЕНЩЂЕуЭМШчЭМЃК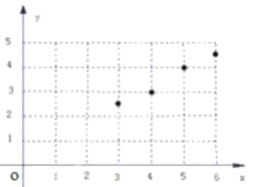 ЃЌгЩЭМПЩжЊГі
ЃЌгЩЭМПЩжЊГі![]() ЪЧЯпадЯрЙи
ЪЧЯпадЯрЙи
ЃЈ2ЃЉгЩЖдееЪ§ОнЃЌМЦЫуЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЛиЙщЗНГЬЯЕЪ§ЮЊ
ЛиЙщЗНГЬЯЕЪ§ЮЊ![]()
![]() ЃЌ
ЃЌ![]()
![]() ,
,![]() ЫљЧѓЯпадЛиЙщЗНГЬЮЊ
ЫљЧѓЯпадЛиЙщЗНГЬЮЊ![]()
![]() .
.
ЃЈ3ЃЉгЩЃЈ2ЃЉЕФЯпадЛиЙщЗНГЬЃЌЙРМЦЩњВњ![]() ЖжМзВњЦЗЕФЩњВњФмКФЮЊ
ЖжМзВњЦЗЕФЩњВњФмКФЮЊ![]() ЃЈЖжЃЉЃЌ
ЃЈЖжЃЉЃЌ![]() ЖжЃЌдЄВтБШММИФЧАНЕЕЭСЫ
ЖжЃЌдЄВтБШММИФЧАНЕЕЭСЫ![]() ЖжБъзМУК.
ЖжБъзМУК.
ЁОЗНЗЈЕуЧчЁПБОЬтжївЊПМВщЩЂЕуЭМЕФЛЗЈКЭЯпадЛиЙщЗНГЬЃЌЪєгкФбЬт.ЧѓЛиЙщжБЯпЗНГЬЕФВНжшЃКЂйвРОнбљБОЪ§ОнЛГіЩЂЕуЭМЃЌШЗЖЈСНИіБфСПОпгаЯпадЯрЙиЙиЯЕЃЛЂкМЦЫу![]() ЕФжЕЃЛЂлМЦЫуЛиЙщЯЕЪ§
ЕФжЕЃЛЂлМЦЫуЛиЙщЯЕЪ§![]() ЃЛЂмаДГіЛиЙщжБЯпЗНГЬЮЊ
ЃЛЂмаДГіЛиЙщжБЯпЗНГЬЮЊ![]() ЃЛ ЛиЙщжБЯпЙ§бљБОЕужааФ
ЃЛ ЛиЙщжБЯпЙ§бљБОЕужааФ![]() ЪЧвЛЬѕживЊаджЪЃЌРћгУЯпадЛиЙщЗНГЬПЩвдЙРМЦзмЬхЃЌАяжњЮвУЧЗжЮіСНИіБфСПЕФБфЛЏЧїЪЦ.
ЪЧвЛЬѕживЊаджЪЃЌРћгУЯпадЛиЙщЗНГЬПЩвдЙРМЦзмЬхЃЌАяжњЮвУЧЗжЮіСНИіБфСПЕФБфЛЏЧїЪЦ.

 бЇЦкИДЯАвЛБОЭЈбЇЯАзмЖЏдБЦкФЉМгЪюМйбгБпШЫУёГіАцЩчЯЕСаД№АИ
бЇЦкИДЯАвЛБОЭЈбЇЯАзмЖЏдБЦкФЉМгЪюМйбгБпШЫУёГіАцЩчЯЕСаД№АИ УЂЙћНЬИЈЪюМйЬьЕижиЧьГіАцЩчЯЕСаД№АИ
УЂЙћНЬИЈЪюМйЬьЕижиЧьГіАцЩчЯЕСаД№АИ