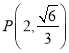题目内容
【题目】函数
， 
．
（Ⅰ）讨论
的极值点的个数；
（Ⅱ）若对于任意
，总有
成立，求实数
的取值范围.
【答案】（Ⅰ）见解析; （Ⅱ）
.
【解析】试题分析：（Ⅰ）求
的导数
，根据
求出
的值域，讨论
的值得出
的正负情况，判断
的单调性和极值点问题；（Ⅱ） 
等价于
，由
，利用分离常数法求出
的表达式，再构造函数求最值即可求出结果.
试题解析：
（Ⅰ）
, 
,
①当
，即
时， 
对
恒成立， 
在
单调增， 
没有极值点；
②当
，即
时，方程
有两个不等正数解
，
不妨设
，则当
时， 
增； 
时， 
减； 
时， 
增，所以
分别为
极大值点和极小值点， 
有两个极值点.
综上所述，当
时， 
没有极值点；当
时， 
有两个极值点.
（Ⅱ）
，由
，即
对于
恒成立，设
，
，
， 
时， 
减， 
时， 
增，
， 
．
练习册系列答案
作业辅导系列答案
相关题目
【题目】2016年巴西奥运会的周边商品有80%左右为“中国制造”,所有的厂家都是经过层层筛选才能获此殊荣．甲、乙两厂生产同一产品，为了解甲、乙两厂的产品质量，以确定这一产品最终的供货商，采用分层抽样的方法从甲、乙两厂生产的产品共98件中分别抽取9件和5件，测量产品中的微量元素的含量（单位：毫克）．下表是从乙厂抽取的5件产品的测量数据：
编号 | 1 | 2 | 3 | 4 | 5 |
| 169 | 178 | 166 | 175 | 180 |
| 75 | 80 | 77 | 70 | 81 |
（1）求乙厂生产的产品数量：
（2）当产品中的微量元素
满足：
，且
时，该产品为优等品．用上述样本数据估计乙厂生产的优等品的数量：
（3）从乙厂抽出的上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数的分布列及数学期望．
