题目内容
【题目】已知椭圆C的两个焦点是F1（﹣2，0），F2（2，0），且椭圆C经过点A（0， 
）．
（1）求椭圆C的标准方程；
（2）若过椭圆C的左焦点F1（﹣2，0）且斜率为1的直线l与椭圆C交于P、Q两点，求线段PQ的长．
【答案】(1) 
(2) 
【解析】试题分析： 
由题意可得椭圆的焦点在
轴上，设椭圆方程为
,由题意可得
求得
,即可得到所求椭圆方程。
求出直线
的方程，代入椭圆方程，设
， 
，运用韦达定理，由弦长公式计算即可得到所求值。
解析：（1）由题意可知椭圆焦点在x轴上，设椭圆方程为
（a＞b＞0），
由题意可知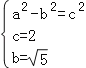
，∴a=3，b=
．
∴椭圆的标准方程为
=1．
（2）直线l的方程为y=x+2，
联立方程组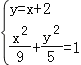
，得14x2+36x﹣9=0，
设P（x1，y1），Q（x2，y2），则x1+x2=﹣
，x1x2=﹣
，
∴|PQ|=
|x1﹣x2|=
=
=
．
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量（
吨）与相应的生产能耗
（吨）标准煤的几组对照数据：
|
|
|
|
|
|
|
|
|
|
（1）请画出上表数据的散点图；并指出
是否线性相关；
（2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（3）已知该厂技术改造前
吨甲产品能耗为
吨标准煤，试根据求出的线性回归方程，预测生产
吨甲产品的生产能耗比技术改造前降低多少吨标准煤？
（参考:用最小二乘法求线性回归方程系数公式 ，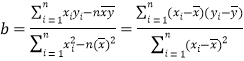
, 
.
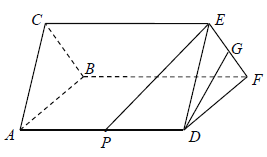
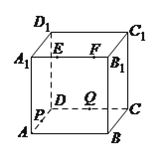
【题目】如图，正方体
的棱长为
，动点
、
在棱
上，动点
，
分别在棱
，
上，若
，
，
，
（
，
，
大于零），则四面体
的体积（ ）．
A. 与，，都有关 B. 与有关，与，无关
C. 与有关，与，无关 D. 与有关，与，无关
【题目】某科技公司生产一种手机加密芯片，其质量按测试指标划分为：指标大于或等于
为合格品，小于为次品．现随机抽取这种芯片共
件进行检测，检测结果统计如表：
测试指标 |
|
|
|
|
|
芯片数量（件） |
|
|
|
|
|
已知生产一件芯片，若是合格品可盈利
元，若是次品则亏损
元.
（Ⅰ）试估计生产一件芯片为合格品的概率；并求生产
件芯片所获得的利润不少于
元的概率.
（Ⅱ）记
为生产
件芯片所得的总利润，求随机变量
的分布列和数学期望
