题目内容
【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，已知
．
（1）求角B的大小；
（2）若a+c=1，求b的取值范围．
【答案】(1) 
;(2) 
.
【解析】试题分析; （1）已知等式利用正弦定理，整理后根据
不为0求出
的值，由
为三角形的内角，利用特殊角的三角函数值即可求出B的度数；
（2）由余弦定理列出关系式，变形后将
及
的值代入表示出
，根据
的范围，利用二次函数的性质求出
的范围，即可求出
的范围．
试题解析：（1）由已知得： 
， 由正弦定理，得
，
∵sinA≠0，则
， 即
，又B∈（0，π），
则B=
.
（2）∵a+c=1，即c=1﹣a，cosB=
，∴由余弦定理得：b2=a2+c2﹣2accosB，即
b2=a2+c2﹣ac=（a+c）2﹣3ac=1﹣3a（1﹣a）
=3（a﹣）2+
，由0＜a＜1，得≤b2＜1，∴≤b＜1．
练习册系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量（
吨）与相应的生产能耗
（吨）标准煤的几组对照数据：
|
|
|
|
|
|
|
|
|
|
（1）请画出上表数据的散点图；并指出
是否线性相关；
（2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（3）已知该厂技术改造前
吨甲产品能耗为
吨标准煤，试根据求出的线性回归方程，预测生产
吨甲产品的生产能耗比技术改造前降低多少吨标准煤？
（参考:用最小二乘法求线性回归方程系数公式 ，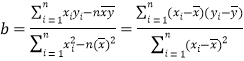
, 
.
