题目内容
已知数列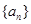 的前
的前 项和为
项和为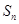 ,且
,且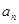 是
是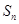 和
和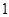 的等差中项,等差数列
的等差中项,等差数列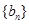 满足
满足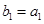 ,
, .
.
(1)求数列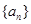 、
、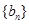 的通项公式;
的通项公式;
(2)设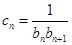 ,数列
,数列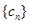 的前
的前 项和为
项和为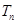 ,求
,求 的取值范围.
的取值范围.
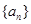 的前
的前 项和为
项和为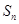 ,且
,且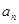 是
是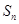 和
和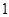 的等差中项,等差数列
的等差中项,等差数列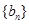 满足
满足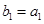 ,
, .
.(1)求数列
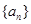 、
、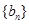 的通项公式;
的通项公式; (2)设
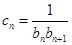 ,数列
,数列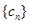 的前
的前 项和为
项和为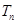 ,求
,求 的取值范围.
的取值范围.(1) ,
, ;(2)
;(2)
 ,
, ;(2)
;(2)
试题分析:(1)由已知得
 ,再利用
,再利用 的关系,将其转化为关于
的关系,将其转化为关于 的递推式,得
的递推式,得 ,故数列
,故数列 是公比为2的等比数列,进而求其通项公式,等差数列
是公比为2的等比数列,进而求其通项公式,等差数列 中,由于知道两项,先求首项和公差,进而求通项公式;(2)求数列前n项和,先考虑其通项公式,根据通项公式的特点,选择相应的求和方法,该题
中,由于知道两项,先求首项和公差,进而求通项公式;(2)求数列前n项和,先考虑其通项公式,根据通项公式的特点,选择相应的求和方法,该题 ,故可采取裂项相消法,求得
,故可采取裂项相消法,求得 ,看作自变量为
,看作自变量为 的函数,进而求值域得
的函数,进而求值域得 的取值范围.
的取值范围.试题解析:(1)∵
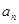 是
是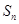 和
和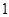 的等差中项,∴
的等差中项,∴ ,当
,当 时,
时, ,∴
,∴
当
 时,
时, , ∴
, ∴ ,即
,即 
∴数列
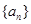 是以
是以 为首项,
为首项, 为公比的等比数列,∴
为公比的等比数列,∴ ,
, ,设
,设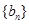 的公差为
的公差为 ,
, ,
, ,∴
,∴ ,∴
,∴ .
.(2)
 ,∴
,∴


 ,∵
,∵  ,∴
,∴ ,
,

 ,∴数列
,∴数列 是一个递增数列 ∴
是一个递增数列 ∴ .
.综上所述,


练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
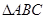 的三边长
的三边长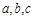 ,满足
,满足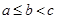
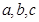 均为正整数,且
均为正整数,且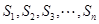 ,且
,且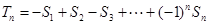 ,求满足不等式
,求满足不等式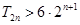 的所有
的所有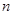 的值;
的值;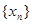 满足
满足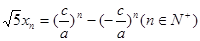 ,证明数列
,证明数列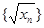 中的任意连续三项为边长均可以构成直角三角形,且
中的任意连续三项为边长均可以构成直角三角形,且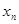 是正整数.
是正整数.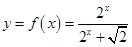 上两点
上两点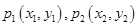 ,若
,若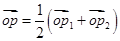 ,且P点的横坐标为
,且P点的横坐标为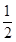 .
.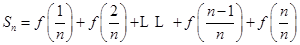 求
求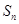 ;
;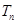 为数列
为数列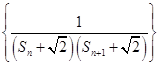 的前n项和,若
的前n项和,若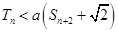 对一切
对一切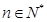 都成立,试求a的取值范围.
都成立,试求a的取值范围. 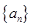 的前
的前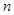 项和为
项和为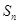 ,且满足
,且满足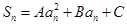 ,其中
,其中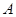 、
、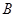 、
、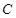 是常数.
是常数.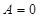 ,
,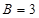 ,
,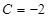 ,求数列
,求数列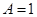 ,
,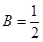 ,
,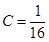 ,且
,且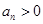 ,求数列
,求数列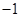 的等比数列.
的等比数列.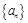 中,
中,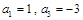 .
.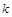 项和
项和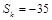 ,求
,求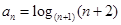
 .我们把使乘积
.我们把使乘积 为整数的数n叫做“优数”,则在区间(1,2004)内的所有优数的和为( )
为整数的数n叫做“优数”,则在区间(1,2004)内的所有优数的和为( ) 满足:
满足: ,
, 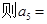 ( )
( )

 满足
满足 ,数列
,数列 是等比数列,且
是等比数列,且 ,则
,则 等于( )
等于( )