题目内容
已知直线l:(2λ+1)x+(λ+2)y+2λ+2=0(λ∈R),有下列四个结论:
①直线l经过定点(0,-2);
②若直线l在x轴和y轴上的截距相等,则λ=1;
③当λ∈[1,4+3
]时,直线l的倾斜角θ∈[120°,135°];
④当λ∈(0,+∞)时,直线l与两坐标轴围成的三角形面积的最小值为
.
其中正确结论的是 (填上你认为正确的所有序号).
①直线l经过定点(0,-2);
②若直线l在x轴和y轴上的截距相等,则λ=1;
③当λ∈[1,4+3
| 3 |
④当λ∈(0,+∞)时,直线l与两坐标轴围成的三角形面积的最小值为
| 8 |
| 9 |
其中正确结论的是
考点:恒过定点的直线
专题:直线与圆
分析:①.以直线l:(2λ+1)x+(λ+2)y+2λ+2=0化为λ(2x+y+2)+(x+2y+2)=0,联立
,解得即可判断出.
②当x=y=0时,解得λ=-1,满足条件;当λ=-2或-
时,不满足条件,舍去.当λ≠-1,-2,-
时,令x=0,解得y=-
,令y=0,解得x=
,由-
=
,解得λ即可判断出.
③当λ∈[1,4+3
]时,直线l的斜率k=tanθ=-
=-2+
,利用λ∈[1,4+3
],可得tanθ∈[-
,-1],解出即可;
④λ∈(0,+∞)时,由②可得S=
|-
|•|-
|=|1-
|,利用基本不等式的性质即可得出.
|
②当x=y=0时,解得λ=-1,满足条件;当λ=-2或-
| 1 |
| 2 |
| 1 |
| 2 |
| 2λ+2 |
| λ+2 |
| -2λ-2 |
| 2λ+1 |
| 2λ+2 |
| λ+2 |
| -2λ-2 |
| 2λ+1 |
③当λ∈[1,4+3
| 3 |
| 2λ+1 |
| λ+2 |
| 3 |
| λ+2 |
| 3 |
| 3 |
④λ∈(0,+∞)时,由②可得S=
| 1 |
| 2 |
| 2λ+2 |
| λ+2 |
| 2λ+2 |
| 2λ+1 |
| 1 | ||
2λ+
|
解答:
解:①.以直线l:(2λ+1)x+(λ+2)y+2λ+2=0化为λ(2x+y+2)+(x+2y+2)=0,联立
,解得x=y=-
.∴直线l过定点(-
,-
).因此不正确.
②当x=y=0时,解得λ=-1,满足条件;当λ=-2或-
时,不满足条件,舍去.当λ≠-1,-2,-
时,令x=0,解得y=-
,令y=0,解得x=
,由-
=
,解得λ=1.综上可得λ±1,因此不正确.
③当λ∈[1,4+3
]时,直线l的斜率k=tanθ=-
=-2+
,∵λ∈[1,4+3
],∴
∈[2-
,1],∴tanθ∈[-
,-1],∵θ∈[0°,180°),∴θ∈[120°,135°],因此直线l的倾斜角θ∈[120°,135°],正确;
④λ∈(0,+∞)时,由②可得S=
|-
|•|-
|=|1-
|≥
,当且仅当λ=1时取等号,因此正确.
综上可得:只有③④正确.
故答案为:③④.
|
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
②当x=y=0时,解得λ=-1,满足条件;当λ=-2或-
| 1 |
| 2 |
| 1 |
| 2 |
| 2λ+2 |
| λ+2 |
| -2λ-2 |
| 2λ+1 |
| 2λ+2 |
| λ+2 |
| -2λ-2 |
| 2λ+1 |
③当λ∈[1,4+3
| 3 |
| 2λ+1 |
| λ+2 |
| 3 |
| λ+2 |
| 3 |
| 3 |
| λ+2 |
| 3 |
| 3 |
④λ∈(0,+∞)时,由②可得S=
| 1 |
| 2 |
| 2λ+2 |
| λ+2 |
| 2λ+2 |
| 2λ+1 |
| 1 | ||
2λ+
|
| 8 |
| 9 |
综上可得:只有③④正确.
故答案为:③④.
点评:本题综合考查了直线恒过定点问题、直线的截距式、倾斜角与斜率之间的关系、三角形的面积计算公式、基本不等式的性质、函数的单调性等基础知识与基本技能方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
函数y=
的图象大致是( )
| x3 |
| 3x-1 |
A、 |
B、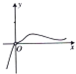 |
C、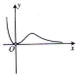 |
D、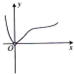 |