题目内容
10.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点坐标为F1(-1,0),且离心率e=$\frac{1}{2}$,求椭圆方程.分析 由已知得:$c=1.e=\frac{c}{a}=\frac{1}{2}$,由此能求出椭圆方程.
解答 解:∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点坐标为F1(-1,0),且离心率e=$\frac{1}{2}$,
∴由已知得:$c=1.e=\frac{c}{a}=\frac{1}{2}$,…(4分)
解得$a=2,b=\sqrt{{a^2}-{c^2}}=\sqrt{3}$…(8分)
∴所求椭圆方程为:$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(10分)
点评 本题考查椭圆方程的求法,是基础题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
相关题目
1.设f1(x)=$\frac{2}{1+x}$,fn+1(x)=f1(fn(x)),且an=$\frac{{f}_{n}(0)-1}{{f}_{n}(0)+2}$,则a2014的值为( )
| A. | (-$\frac{1}{2}$)2015 | B. | ($\frac{1}{2}$)2015 | C. | ($\frac{1}{2}$)2014 | D. | (-$\frac{1}{2}$)2014 |
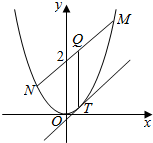 已知抛物线C:x${\;}^{2}=\frac{1}{2}y$,直线y=kx+2交C于M、N两点,Q是线段MN的中点,过Q作x轴的垂线交C于点T.
已知抛物线C:x${\;}^{2}=\frac{1}{2}y$,直线y=kx+2交C于M、N两点,Q是线段MN的中点,过Q作x轴的垂线交C于点T.