题目内容
有红、蓝、黄、绿四种颜色的球各6个，每种颜色的6个球分别标有数字1、2、3、4、5、6，从中任取3个标号不同的球，这3个颜色互不相同且所标数字互不相邻的取法种数为 ．
考点：计数原理的应用
专题：排列组合
分析：所标数字互不相邻的方法有4种，这3种颜色互不相同有C43A33种，根据分步计数原理，即可求出颜色互不相同且所标数字互不相邻的取法种数．
解答：
解：所标数字互不相邻的方法有：135，136，146，246，共4种方法．
这3种颜色互不相同有C43A33=4×3×2×1=24种，
∴这3种颜色互不相同且所标数字互不相邻的有4×24=96种．
故答案为：96．
这3种颜色互不相同有C43A33=4×3×2×1=24种，
∴这3种颜色互不相同且所标数字互不相邻的有4×24=96种．
故答案为：96．
点评：本题主要考查了排列组合，以及两个基本原理的应用，解题的关键是不重不漏，属于中档题．
练习册系列答案
智能训练练测考系列答案
相关题目
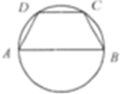如图，已知AB=2c（2c为常数且c＞0）．以AB为直径的圆有一内接梯形ABCD，且AB∥CD．若椭圆以A、B为焦点．且过C、D两点，则当梯形ABCD的面积最大时，椭圆的离心率为