题目内容
在学校组织的趣味数学知识竞赛中,甲、乙两队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束,根据分组情况知除第五局甲队获胜的概率是
外,其余每局比赛甲队获胜的概率都是
,假设各局比赛结果相互对立.
(1)分别求乙队以3:0,3:1,3:2获胜的概率;
(2)若比赛结果为3:0或3:1,则胜利方得3分、对方得0分;若比赛结果为3:2,则胜利方得2分、对方得1分.求甲队得分X的分布列及数学期望.
| 1 |
| 2 |
| 2 |
| 3 |
(1)分别求乙队以3:0,3:1,3:2获胜的概率;
(2)若比赛结果为3:0或3:1,则胜利方得3分、对方得0分;若比赛结果为3:2,则胜利方得2分、对方得1分.求甲队得分X的分布列及数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:计算题,概率与统计
分析:(1)乙队获胜有三种情形,①3:0,②3:1,③3:2,其每种情形的最后一局肯定是乙队胜,分别求出相应的概率,最后根据互斥事件的概率公式求出乙队获得这次比赛胜利的概率;
(2)X的取值可能为0,1,2,3,然后利用相互独立事件的概率乘法公式求出相应的概率,列出分布列,最后根据数学期望公式解之即可.
(2)X的取值可能为0,1,2,3,然后利用相互独立事件的概率乘法公式求出相应的概率,列出分布列,最后根据数学期望公式解之即可.
解答:
解:(1)乙队获胜有三种情形,其每种情形的最后一局肯定是乙队胜
①3:0,概率为P1=(
)3=
;
②3:1,概率为P2=
(
)2×(1-
)×
=
;
③3:2,概率为P3=
(
)2×(1-
)2×
=
,
∴甲队3:0,3:1,3:2胜利的概率:
,
,
.
(2)甲队得分X,则X的取值可能为0,1,2,3.
由(1)知P(X=0)=P1+P2=
;
P(X=1)=P3=
;
P(X=2)=
(
)2×(1-
)2×
=
;
P(X=3)=(1-
)3+
(1-
)2×(
)×
=
;
则X的分布列为
E(X)=3×
+2×
+1×
+0×
=
.
①3:0,概率为P1=(
| 1 |
| 3 |
| 1 |
| 27 |
②3:1,概率为P2=
| C | 2 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 27 |
③3:2,概率为P3=
| C | 2 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 27 |
∴甲队3:0,3:1,3:2胜利的概率:
| 1 |
| 27 |
| 2 |
| 27 |
| 4 |
| 27 |
(2)甲队得分X,则X的取值可能为0,1,2,3.
由(1)知P(X=0)=P1+P2=
| 3 |
| 27 |
P(X=1)=P3=
| 4 |
| 27 |
P(X=2)=
| C | 2 4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 4 |
| 27 |
P(X=3)=(1-
| 1 |
| 3 |
| C | 1 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 16 |
| 27 |
则X的分布列为
| X | 3 | 2 | 1 | 0 | ||||||||
| P |
|
|
|
|
| 16 |
| 27 |
| 4 |
| 27 |
| 4 |
| 27 |
| 3 |
| 27 |
| 20 |
| 9 |
点评:本题主要考查了相互独立事件的概率乘法公式,以及离散型随机变量的期望与分布列,同时考查了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=2x-1-log
x,则f(x)的零点的个数为( )
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
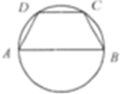 如图,已知AB=2c(2c为常数且c>0).以AB为直径的圆有一内接梯形ABCD,且AB∥CD.若椭圆以A、B为焦点.且过C、D两点,则当梯形ABCD的面积最大时,椭圆的离心率为
如图,已知AB=2c(2c为常数且c>0).以AB为直径的圆有一内接梯形ABCD,且AB∥CD.若椭圆以A、B为焦点.且过C、D两点,则当梯形ABCD的面积最大时,椭圆的离心率为