题目内容
14.设$a={log_5}4,b={log_{\sqrt{2}}}3,c={({{{log}_{0.2}}3})^2}$,则a,b,c的大小关系为( )| A. | a>b>c | B. | b>c>a | C. | a>c>b | D. | b>a>c |
分析 a=log54∈(0,1),b=$lo{g}_{\sqrt{2}}3$>1,c=$(lo{g}_{0.2}3)^{2}$=$(lo{g}_{5}3)^{2}$<log53<log54,即可得出.
解答 解:∵a=log54∈(0,1),b=$lo{g}_{\sqrt{2}}3$>1,c=$(lo{g}_{0.2}3)^{2}$=$(lo{g}_{5}3)^{2}$<log53<log54,
∴b>a>c.
故选:D.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
5.执行如图所示的程序框图,输出的n值为( )
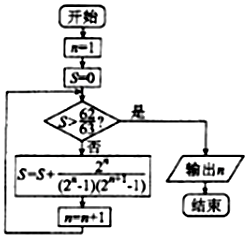

| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
2.若复数z满足(1+i)z=2i,其中i为虚数单位,则$\overline z$( )
| A. | 1-i | B. | 1+i | C. | 2-2i | D. | 2+2i |
9.已知($\overline{z}$-1+3i)(2-i)=4+3i(其中i是虚数单位),则z的虚部为( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
6.执行如图的程序框图,则输出x的值是( )
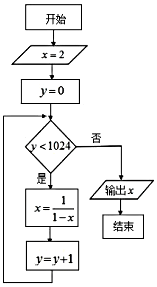

| A. | 2016 | B. | 1024 | C. | $\frac{1}{2}$ | D. | -1 |
 ,求证:
,求证: .
.