题目内容
变量x,y满足约束条件
,则s=
的取值范围是( )
|
| 2y+2 |
| x+1 |
| A、[1,4] |
| B、[2,8] |
| C、[2,10] |
| D、[3,9] |
考点:简单线性规划
专题:不等式的解法及应用
分析:先根据约束条件
画出可行域,设s=
,再利用s的几何意义求最值,只需求出过定点(-1,-1)直线过可行域内的点A时,斜率的值即可.
|
| 2y+2 |
| x+1 |
解答:
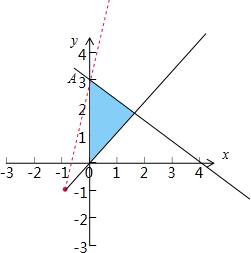 解:先根据约束条件
解:先根据约束条件
画出可行域,
s=
=2×
,表示可行域内的点到(-1,-1)连线的斜率的2倍:2×
=8,
s的最大值为过定点(-1,-1)与A(0,3)的直线的斜率的2倍:,
当直线与y=x重合时,s最小,最小值为:2.
s的范围[2,8]
故选:B.
 解:先根据约束条件
解:先根据约束条件
|
s=
| 2y+2 |
| x+1 |
| y+1 |
| x+1 |
| 3+1 |
| 0+1 |
s的最大值为过定点(-1,-1)与A(0,3)的直线的斜率的2倍:,
当直线与y=x重合时,s最小,最小值为:2.
s的范围[2,8]
故选:B.
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.巧妙识别目标函数的几何意义是我们研究规划问题的基础.

练习册系列答案
相关题目
在△ABC中,若
•
=-2,且∠B=60°,则△ABC面积为( )
| AB |
| BC |
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
已知某几何体的三视图如图所示.则该几何体的体积是( )


A、
| ||||
B、
| ||||
C、
| ||||
| D、4 |
复数Z=1+
i,则|Z4|=( )
| 3 |
| A、16 | B、8 | C、4 | D、2 |
设m,n是两条异面直线,P是空间任一点.下列命题中正确的是( )
| A、过m且与n平行的平面有且只有一个 |
| B、过m且与n垂直的平面有且只有一个 |
| C、m与n所成的角的范围是(0,π) |
| D、过P与m、n均平行的平面有且只有一个 |
设α、β是方程4x2-4mx+m+2=0有两个不相等的实数根,则以下哪个k的值满足要求( )
| A、0 | B、-1 | C、4 | D、2 |