题目内容
13．已知sin（540°+α）=-$\frac{4}{5}$，则cos（α-270°）=（ ）| A． | $\frac{4}{5}$ | B． | -$\frac{4}{5}$ | C． | $\frac{3}{5}$ | D． | $-\frac{3}{5}$ |
分析 先利用sin（k•360°+α）=sinα化简sin（540°+α），再利用诱导公式化简求出sinα的值，同理化简cos（α-270°）可得答案．
解答 解：根据sin（k•360°+α）=sinα公式，
将sin（540°+α）化简为：
sin（540°+α）=sin（360°+180°+α）=（sin180°+α）=-sinα=-$\frac{4}{5}$，
可得：sinα=$\frac{4}{5}$，
那么：cos（α-270°）=cos（270°-α）=-sina=-$\frac{4}{5}$，
故选B．
点评 本题考查的知识点是诱导公式，难度不大，属于基础题
练习册系列答案
相关题目
17．将函数f（x）=2sin（ωx+$\frac{π}{4}$）（ω＞0）的图象向右平移$\frac{π}{4ω}$个单位，得到函数y=g（x）的图象，若y=g（x）在[-$\frac{π}{6}$，$\frac{π}{3}$]上为增函数，则ω的最大值为（ ）
| A． | 3 | B． | 2 | C． | $\frac{3}{2}$ | D． | $\frac{5}{4}$ |
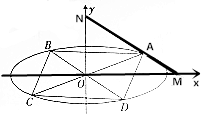已知椭圆O：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点（$\sqrt{3}$，-$\frac{1}{2}$），A（x0，y0）（x0y0≠0），其上顶点到直线$\sqrt{3}$x+y+3=0的距离为2，过点A的直线l与x，y轴的交点分别为M、N，且$\overrightarrow{AN}$=2$\overrightarrow{MA}$．
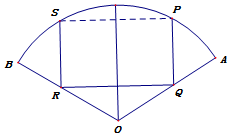如图，扇形OAB的半径为1，圆心角为120°，四边形PQRS是扇形的内接矩形，当其面积最大时，求点P的位置，并求此最大面积．
2．已知i是虚数单位，若z（1+i）=1+3i，则z=（ ）
| A． | 2+i | B． | 2-i | C． | -1+i | D． | -1-i |