题目内容
5.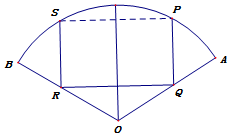 如图,扇形OAB的半径为1,圆心角为120°,四边形PQRS是扇形的内接矩形,当其面积最大时,求点P的位置,并求此最大面积.
如图,扇形OAB的半径为1,圆心角为120°,四边形PQRS是扇形的内接矩形,当其面积最大时,求点P的位置,并求此最大面积.
分析 根据题意,设SP中点为C,PQ中点为D,∠COP=θ,表示出四边形SPRS的面积,
再利用三角恒等变换求出它的最大值即可.
解答 解:设SP中点为C,PQ中点为D,如图所示;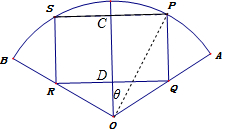
设∠COP=θ,则CP=1×sinθ=sinθ,
CO=cosθ,
DQ=CP=sinθ,
又∠DOQ=$\frac{π}{3}$,
∴OD=$\frac{sinθ}{\sqrt{3}}$,
∴CD=OC-OD=cosθ-$\frac{sinθ}{\sqrt{3}}$,
∴S四边形PQRS=CD×SP
=(cosθ-$\frac{sinθ}{\sqrt{3}}$)•2sinθ
=sin2θ-$\frac{{2sin}^{2}θ}{\sqrt{3}}$
=sinθ-$\frac{1-cos2θ}{\sqrt{3}}$
=sin2θ+$\frac{1}{\sqrt{3}}$cos2θ-$\frac{1}{\sqrt{3}}$
=$\frac{2\sqrt{3}}{3}$sin(2θ+$\frac{π}{6}$)-$\frac{\sqrt{3}}{3}$,
当θ=$\frac{π}{6}$时,四边形SPQR取得最大值为
Smax=$\frac{\sqrt{3}}{3}$,
此时点P在弧AB的四等分点处.
点评 本题考查了三角恒等变换以及三角函数的应用问题,是综合性题目.

练习册系列答案
相关题目
9.已知集合A={x|x(x-3)<0},B={-1,0,1,2,3},则A∩B=( )
| A. | {-1} | B. | {1,2} | C. | {0,3} | D. | {-1,1,2,3} |
13.已知sin(540°+α)=-$\frac{4}{5}$,则cos(α-270°)=( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
15.函数$f(x)=\frac{{\sqrt{3}+tanx}}{{1-\sqrt{3}tanx}}$( )
| A. | 定义域是$\{x|x≠kπ+\frac{π}{6},(k∈Z)\}$ | B. | 值域是R | ||
| C. | 在其定义域上是增函数 | D. | 最小正周期是π |