题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{\frac{{2}^{x}+2}{2},x≤1}\\{|lo{g}_{2}(x-1)|,x>1}\end{array}\right.$,则函数F(x)=f[f(x)]-2f(x)-$\frac{3}{2}$的零点个数是( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 令t=f(x),F(x)=0,则f(t)-2t-$\frac{3}{2}$=0,分别作出y=f(x)和直线y=2x+$\frac{3}{2}$,得到两交点的横坐标,再由图象观察,即可得到所求零点个数.
解答 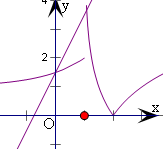 解:令t=f(x),F(x)=0,
解:令t=f(x),F(x)=0,
则f(t)-2t-$\frac{3}{2}$=0,
分别作出y=f(x)和直线y=2x+$\frac{3}{2}$,
由图象可得有两个交点,横坐标设为t1,t2,
则t1=0,1<t2<2,
即有f(x)=0有一根;
1<f(x)<2时,t2=f(x)有3个不等实根,
综上可得F(x)=0的实根个数为4,
即函数F(x)=f[f(x)]-2f(x)-$\frac{3}{2}$的零点个数是4.
故选:A.
点评 本题考查函数的零点个数问题解法,注意运用转化思想和换元法,以及数形结合思想方法,考查判断和观察能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.已知i是虚数单位,复数i•z=1-2i,则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知抛物线C:y2=2px(p>0),过其焦点F的直线l交抛物线C于点A、B,|AF|=3|BF|,则|AB|=( )
| A. | p | B. | $\frac{4}{3}p$ | C. | 2p | D. | $\frac{8}{3}p$ |
13.已知sin(540°+α)=-$\frac{4}{5}$,则cos(α-270°)=( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |