题目内容
1. 已知椭圆O:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点($\sqrt{3}$,-$\frac{1}{2}$),A(x0,y0)(x0y0≠0),其上顶点到直线$\sqrt{3}$x+y+3=0的距离为2,过点A的直线l与x,y轴的交点分别为M、N,且$\overrightarrow{AN}$=2$\overrightarrow{MA}$.
已知椭圆O:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点($\sqrt{3}$,-$\frac{1}{2}$),A(x0,y0)(x0y0≠0),其上顶点到直线$\sqrt{3}$x+y+3=0的距离为2,过点A的直线l与x,y轴的交点分别为M、N,且$\overrightarrow{AN}$=2$\overrightarrow{MA}$.(1)证明:|MN|为定值;
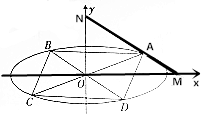
(2)如图所示,若A,C关于原点对称,B,D关于原点对称,且$\overrightarrow{BD}$=λ$\overrightarrow{NM}$,求四边形ABCD面积的最大值.
分析 (1)其上顶点(0,b)到直线$\sqrt{3}$x+y+3=0的距离为2,利用点到直线的距离公式可得$\frac{b+3}{2}=2$,根据椭圆O:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点($\sqrt{3}$,-$\frac{1}{2}$),解得a2.可得椭圆的标准方程为:$\frac{{x}^{2}}{4}+{y}^{2}$=1.设经过点A的直线方程为:y-y0=k(x-x0),可得M$({x}_{0}-\frac{{y}_{0}}{k},0)$,N(0,y0-kx0).利用$\overrightarrow{AN}$=2$\overrightarrow{MA}$,可得k=-$\frac{2{y}_{0}}{{x}_{0}}$.利用两点之间的距离公式可得|MN|.
(2)设∠AOD=α.由$\overrightarrow{BD}$=λ$\overrightarrow{NM}$,可得2|OD|=3λ.由题意可得:S四边形ABCD=$4×\frac{1}{2}|OA|•|OD|sinα$=2×$\frac{3λ}{2}$|OA|•sinα,即可得出.
解答 (1)证明:其上顶点(0,b)到直线$\sqrt{3}$x+y+3=0的距离为2,∴$\frac{b+3}{2}=2$,解得b=1.
又椭圆O:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点($\sqrt{3}$,-$\frac{1}{2}$),∴$\frac{3}{{a}^{2}}+\frac{1}{4}$=1,解得a2=4.
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+{y}^{2}$=1.
点A在椭圆上,∴$\frac{{x}_{0}^{2}}{4}+{y}_{0}^{2}$=1.
设经过点A的直线方程为:y-y0=k(x-x0),
可得M$({x}_{0}-\frac{{y}_{0}}{k},0)$,N(0,y0-kx0).
∵$\overrightarrow{AN}$=2$\overrightarrow{MA}$,∴-x0=$\frac{2{y}_{0}}{k}$,即k=-$\frac{2{y}_{0}}{{x}_{0}}$.
∴|MN|=$\sqrt{({x}_{0}-\frac{{y}_{0}}{k})^{2}+({y}_{0}-k{x}_{0})^{2}}$=$\sqrt{\frac{9}{4}{x}_{0}^{2}+9{y}_{0}^{2}}$=3为定值.
(2)解:设∠AOD=α.∵$\overrightarrow{BD}$=λ$\overrightarrow{NM}$,∴2|OD|=3λ.
由题意可得:S四边形ABCD=$4×\frac{1}{2}|OA|•|OD|sinα$=2×$\frac{3λ}{2}$|OA|•sinα≤3λ|OA|.
点评 本题考查题意的标准方程及其性质、向量共线定理及其坐标运算性质、点到直线的距离公式、三角形面积就算公式,考查了推理能力与计算能力,属于难题.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
| A. | (-3,2,5) | B. | (-3,-2,5) | C. | (3,-2,-5) | D. | (-3,2,-5) |
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点F1,F2,离心率$e=\frac{{\sqrt{2}}}{2}$,短轴长为2.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点F1,F2,离心率$e=\frac{{\sqrt{2}}}{2}$,短轴长为2.