题目内容
11.在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为$\frac{\sqrt{3}}{2}$,以原点为圆心,以椭圆C的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切,过点F2的直线l与椭圆C相交于M,N两点.(1)求椭圆C的方程;
(2)若$\overrightarrow{MF_2}$=3$\overrightarrow{F_2N}$,求直线l的方程;
(3)求△F1MN面积的最大值.
分析 (1)运用离心率公式和直线与相切的条件:d=r,结合a,b,c的关系,解得a,进而得到椭圆方程;
(2)求得右焦点,设出M(x1,y1),N(x2,y2),设直线l:x=my+$\sqrt{3}$,代入椭圆方程,运用韦达定理和向量共线的坐标表示,解方程可得m,进而得到直线的方程;
(3)运用弦长公式和换元法,运用三角形的面积公式可得S=$\frac{1}{2}$•2c•|y1-y2|,化简整理运用基本不等式,即可得到最大值.
解答 解:(1)由题意可得e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
由直线x-y+$\sqrt{2}$=0与圆x2+y2=b2相切,可得
$\frac{\sqrt{2}}{\sqrt{1+1}}$=b=1,
又a2-c2=1,
解得a=2,c=$\sqrt{3}$,
即有椭圆的方程为$\frac{{x}^{2}}{4}$+y2=1;
(2)F2($\sqrt{3}$,0),
设M(x1,y1),N(x2,y2),
设直线l:x=my+$\sqrt{3}$,代入椭圆方程可得,
(4+m2)y2+2$\sqrt{3}$my-1=0,
y1+y2=-$\frac{2\sqrt{3}m}{4+{m}^{2}}$,y1y2=-$\frac{1}{4+{m}^{2}}$,
由$\overrightarrow{MF_2}$=3$\overrightarrow{F_2N}$,可得y1=-3y2,
解方程可得m=±$\frac{\sqrt{2}}{2}$,
即有直线l的方程为x=±$\frac{\sqrt{2}}{2}$y+$\sqrt{3}$;
(3)△F1MN面积为S=$\frac{1}{2}$•2c•|y1-y2|=$\sqrt{3}$•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$
=$\sqrt{3}$•$\sqrt{\frac{12{m}^{2}}{(4+{m}^{2})^{2}}+\frac{4}{4+{m}^{2}}}$=$\sqrt{3}$•$\frac{4\sqrt{1+{m}^{2}}}{4+{m}^{2}}$,
令1+m2=t(t≥1),则S=4$\sqrt{3}$•$\frac{1}{\sqrt{t}+\frac{3}{\sqrt{t}}}$≤4$\sqrt{3}$•$\frac{1}{2\sqrt{3}}$=2,
当t=3,即m=±$\sqrt{2}$时,S取得最大值,且为2.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和直线与圆相切的条件,考查向量共线的坐标表示,以及直线方程和椭圆方程联立,运用韦达定理和弦长公式,考查化简整理的运算能力,属于中档题.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案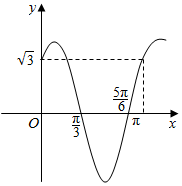 若函数y=Asin(ωx+φ)的图象如图所示,求它的解析式、频率和振幅.
若函数y=Asin(ωx+φ)的图象如图所示,求它的解析式、频率和振幅. 已知△ABC与△DBC都是边长为$\frac{{2\sqrt{3}}}{3}$的等边三角形,且平面ABC⊥平面DBC,过点A作PA⊥平面ABC,且AP=2.
已知△ABC与△DBC都是边长为$\frac{{2\sqrt{3}}}{3}$的等边三角形,且平面ABC⊥平面DBC,过点A作PA⊥平面ABC,且AP=2.