题目内容
设f(x)=ax+b,其中a,b为实数,f1(x)=f(x),fn+1(x)=f(fn(x)),n=1,2,3,…若f7(x)=128x+508,则a+b=( )
| A、6 | B、7 | C、8 | D、9 |
考点:函数的值
专题:函数的性质及应用
分析:利用待定系数法求出f7(x)的表达式,建立方程组即可得到结论.
解答:
解:∵f(x)=ax+b,
∴f1(x)=f(x)=ax+b,
f2(x)=f[f(x)]=a(ax+b)+b=a2x+b(a+1),
f3(x)=f[f2(x)]=a[a2x+b(a+1)]+b=a3x+ab(a+1)+b=a3x+b(a2+a+1),
f4(x)=f[f3(x)]=a[a3x+b(a2+a+1)]+b=a4•x+b(a3+a2+a+1),
…
f7(x)=f[f6(x)]=a7•x+b(a6+…+a2+a+1),
∵f7(x)=128x+508,
∴a7=128,b(a6+…+a2+a+1)=
=508,
解得a=2,b=4,
故a+b=6,
故选:A
∴f1(x)=f(x)=ax+b,
f2(x)=f[f(x)]=a(ax+b)+b=a2x+b(a+1),
f3(x)=f[f2(x)]=a[a2x+b(a+1)]+b=a3x+ab(a+1)+b=a3x+b(a2+a+1),
f4(x)=f[f3(x)]=a[a3x+b(a2+a+1)]+b=a4•x+b(a3+a2+a+1),
…
f7(x)=f[f6(x)]=a7•x+b(a6+…+a2+a+1),
∵f7(x)=128x+508,
∴a7=128,b(a6+…+a2+a+1)=
| b(1-a7) |
| 1-a |
解得a=2,b=4,
故a+b=6,
故选:A
点评:本题主要考查函数解析式的求法,利用待定系数法是解决本题的关键.

练习册系列答案
相关题目
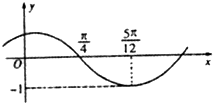 从函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
从函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
等比数列{an}满足a2+a4=20,a3+a5=40,则公比q=( )
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
要得到函数y=sin(2x+
)的图象,只要将函数y=cos2x的图象( )
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
在△ABC中,|AB|=3,|AC|=2,
=
+
,则直线AD通过△ABC的( )
| AD |
| 1 |
| 2 |
| AB |
| 3 |
| 4 |
| AC |
| A、垂心 | B、外心 | C、重心 | D、内心 |
定积分
xdx等于( )
| ∫ | 3 0 |
A、
| ||
| B、9 | ||
| C、8 | ||
| D、3 |
设z1=i5+i6…+i12,z2=i5•i6…i12,则z1,z2的关系是( )
| A、z1=z2 |
| B、z1=-z2 |
| C、z1=z2-1 |
| D、无法确定 |