题目内容
3.设ω>0,若函数f(x)=sin(ωx+$\frac{π}{4}$)的图象向左平移4π个单位与原图象重合,则ω的最小值为$\frac{1}{2}$.分析 由三角函数图象的平移得到平移后所得图象对应的函数解析式,然后利用正弦函数的周期性即可得解.
解答 解:函数f(x)=sin(ωx+$\frac{π}{4}$)(ω>0)的图象向左平移4π个单位得到图象对应的函数解析式为y=sin(ωx+4πω+$\frac{π}{4}$),
∵平移前后的函数图象重合,
∴$\frac{π}{4}$=4πω+$\frac{π}{4}$+2kπ,k∈Z.
∴ω=-$\frac{k}{2}$,k∈Z.
∴ω的最小值是$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了y=Asin(ωx+φ)型函数的图象和性质,考查了三角函数的诱导公式,是基础题.

练习册系列答案
相关题目
12.已知集合A={x∈R|-1<x<3},B={x∈R|-1<x<m+1},若x∈B成立的一个充分不必要条件是x∈A,则实数m的取值范围是( )
| A. | m≥2 | B. | m≤2 | C. | m>2 | D. | -2<m<2 |
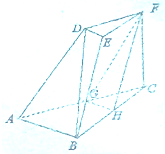 如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.
如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.