题目内容
已知函数f(x)=cos4x-2sinxcosx-sin4x,则f(x)的单调减区间为 .
考点:三角函数中的恒等变换应用,二倍角的正弦,二倍角的余弦
专题:三角函数的图像与性质
分析:对函数解析式合并同类项后,利用二倍角公式和两角和公式化简,然后利用三角函数的性质求得其单调减区间.
解答:
解:∵f(x)=cos4x-2sinxcosx-sin4x
=(cos2x+sin2x)(cos2x-sin2x)-sin2x=cos2x-sin2x
=
(
cos2x-
sin2x)
=
cos(2x+
),
∴当2kπ≤2x+
≤π+2kπ时,即kπ-
≤x≤kπ+
时,k∈Z,函数单调减,
∴函数f(x)的单调递减区间为:[kπ-
,kπ+
](k∈Z),
故答案为:[kπ-
,kπ+
](k∈Z).
=(cos2x+sin2x)(cos2x-sin2x)-sin2x=cos2x-sin2x
=
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 2 |
| π |
| 4 |
∴当2kπ≤2x+
| π |
| 4 |
| π |
| 8 |
| 3π |
| 8 |
∴函数f(x)的单调递减区间为:[kπ-
| π |
| 8 |
| 3π |
| 8 |
故答案为:[kπ-
| π |
| 8 |
| 3π |
| 8 |
点评:本题主要考查三角函数中的恒等变换的应用,三角函数的图象和性质.考查了学生基础知识的掌握.

练习册系列答案
相关题目
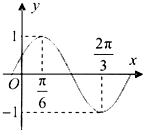 已知函数f(x)=sin(ωx+φ)(ω>0,φ<
已知函数f(x)=sin(ωx+φ)(ω>0,φ<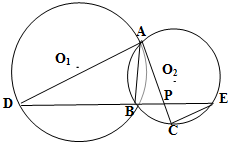 如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.若AD是⊙O2的切线,且PA=6,PC=2,BD=9,AB的长为
如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.若AD是⊙O2的切线,且PA=6,PC=2,BD=9,AB的长为 如图,PC切⊙O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,PC=2,PB=4,则CD=
如图,PC切⊙O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,PC=2,PB=4,则CD=